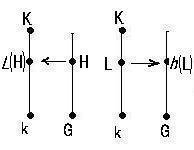
今 K/kを正則な体、Lをその中間体すなわちK⊃L⊃kなる体とする。
定理2.
ガロア群 G(K/k) = G の部分群 H の個数と K/k
の中間体 L の個数とは同数である。
|
さらに詳しくHとLの間に次のようにして1対1の対応をつけることが
できる。これが ガロア理論の基本定理 と呼ばれている定理である。
すなわち
定理3.
正則体 K/k においてガロア群 G の部分群に対して
H の置換により動かないようなKの元の全体L(H)を対
応せしめ、K/k の中間体Lに対してLの要素をすべて
動かさないような G の置換の全体 h(L)を対応せし
めればこれらの対応は互いに逆な対応で、
これによって H と L の1対1の対応がつけられる。
|
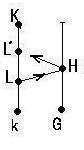
証明:
定理に述べたようにK/kの中間体Lとガロア群の部分群Hとが対応してい
 ることを示すには次の2つの式を証明すればよい。
(*1) Lh(L) = L
(*2) hL(H) = H
(*1) の式は H = h(L) , L(H) = L' と置いたとき
L'=L となることである。
L' は K の要素の中で H によって不変なものの集合であるが、HはLを
不変にする置換の集合であるからL⊂L' が成り立つ。 ることを示すには次の2つの式を証明すればよい。
(*1) Lh(L) = L
(*2) hL(H) = H
(*1) の式は H = h(L) , L(H) = L' と置いたとき
L'=L となることである。
L' は K の要素の中で H によって不変なものの集合であるが、HはLを
不変にする置換の集合であるからL⊂L' が成り立つ。
 次に K の要素 α が H で不変であったとする。
定理1.の証明の第1段によって K/L は正則拡大でそのガロア群は
丁度 H に一致する。
今もし αが Lの要素でなければ L(α)/Lの次数は1より大であり、
したがって恒等置換でないL(α)の L-同型対応が存在する。
定理1.によってこの対応は K/L のガロア置換に延長される。
すなわち K/L のガロア群である H の適当な置換によって、αは恒等
置換と異なる値に写る.これは矛盾であるからα∈Lでなければならない。
以上からL'⊂Lとなるから前に示した L⊂L'と合わせて L=L'=Lh(L)が
得られる。 次に K の要素 α が H で不変であったとする。
定理1.の証明の第1段によって K/L は正則拡大でそのガロア群は
丁度 H に一致する。
今もし αが Lの要素でなければ L(α)/Lの次数は1より大であり、
したがって恒等置換でないL(α)の L-同型対応が存在する。
定理1.によってこの対応は K/L のガロア置換に延長される。
すなわち K/L のガロア群である H の適当な置換によって、αは恒等
置換と異なる値に写る.これは矛盾であるからα∈Lでなければならない。
以上からL'⊂Lとなるから前に示した L⊂L'と合わせて L=L'=Lh(L)が
得られる。
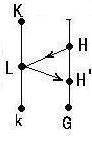 (*2)を証明する際にも先ずL(H)=L,h(L)=H'と置いたとき
H'⊃H なることが前と同様にして得られる。
H'は前にも述べたようにK/Lのガロア群であるからその
位数は [K:L] に等しい。
H の位数をhとしてその要素を σ1,σ2,・・・,σh
と置き、σ1=1 とすれば、K=L(θ)に対して
(*3) f(x)=(x-σ1θ)(x-σ2θ)・・・(x-σhθ)
は σ1θ = θ を根にもつ h 次の多項式である。
f(x) を x の冪に展開して
= xh-α1xh-1+ α2xh-2+・・・+(-1)hαh
と置けば
α1=σ1θ+σ2θ+・・・+σhθ
α2=(σ1θ)(σ2θ)+(σ1θ)(σ3θ)+・・・+(σh-1θ)(σhθ)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
αh=(σ1θ)(σ2θ)・・・(σhθ)
今 σ を H の任意の要素とすればたとえば σα1 は
(一般に σ により L の要素の積は像の積に写されること、
すなわち σ(αβ)=(σα)(σβ)なることに注意して)
σα2
=(σσ1θ)(σσ2θ)+(σσ1θ)(σσ3θ)+・・・+(σσh-1θ)(σσhθ)
同様にσαiはαiの式においてσjθをσσjθによって置き換えて
得られる. したがって
xh-σα1xh-1+ σα2xh-2+・・・・・・+(-1)hσαh
(*4) =(x-σσ1θ)(x-σσ2θ)・・・(x-σσhθ)
しかるに σ∈H であるから
σ1,σ2,・・・,σhとσσ1,σσ2,・・・,σσh は順序を除いて一致する。
したがって(*3)と(*4)は因数の順序を除いて一致し、それらの展開の
係数を比較して
σα1=α1,σα2=α2 , ・・・,σαh=αh
ここに σ は H の任意の要素であるから f(x) の係数 ±αi は L の
要素となり、θはh次のf(x)∈L[x]の根となることが証(明)された。
[K:L]はθの満足するL[x]における既約多項式の次数であるから
[K:L] ≤ h
一方 [K:L] は K/L のガロア群 H' の位数にも等しい。すなわち
H' の位数 ≤ H の位数
が成立し、これはH⊂H'なることから H=H'の場合に限って可能である。
以上から目的の等式 (*2) が証明された。 // (*2)を証明する際にも先ずL(H)=L,h(L)=H'と置いたとき
H'⊃H なることが前と同様にして得られる。
H'は前にも述べたようにK/Lのガロア群であるからその
位数は [K:L] に等しい。
H の位数をhとしてその要素を σ1,σ2,・・・,σh
と置き、σ1=1 とすれば、K=L(θ)に対して
(*3) f(x)=(x-σ1θ)(x-σ2θ)・・・(x-σhθ)
は σ1θ = θ を根にもつ h 次の多項式である。
f(x) を x の冪に展開して
= xh-α1xh-1+ α2xh-2+・・・+(-1)hαh
と置けば
α1=σ1θ+σ2θ+・・・+σhθ
α2=(σ1θ)(σ2θ)+(σ1θ)(σ3θ)+・・・+(σh-1θ)(σhθ)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
αh=(σ1θ)(σ2θ)・・・(σhθ)
今 σ を H の任意の要素とすればたとえば σα1 は
(一般に σ により L の要素の積は像の積に写されること、
すなわち σ(αβ)=(σα)(σβ)なることに注意して)
σα2
=(σσ1θ)(σσ2θ)+(σσ1θ)(σσ3θ)+・・・+(σσh-1θ)(σσhθ)
同様にσαiはαiの式においてσjθをσσjθによって置き換えて
得られる. したがって
xh-σα1xh-1+ σα2xh-2+・・・・・・+(-1)hσαh
(*4) =(x-σσ1θ)(x-σσ2θ)・・・(x-σσhθ)
しかるに σ∈H であるから
σ1,σ2,・・・,σhとσσ1,σσ2,・・・,σσh は順序を除いて一致する。
したがって(*3)と(*4)は因数の順序を除いて一致し、それらの展開の
係数を比較して
σα1=α1,σα2=α2 , ・・・,σαh=αh
ここに σ は H の任意の要素であるから f(x) の係数 ±αi は L の
要素となり、θはh次のf(x)∈L[x]の根となることが証(明)された。
[K:L]はθの満足するL[x]における既約多項式の次数であるから
[K:L] ≤ h
一方 [K:L] は K/L のガロア群 H' の位数にも等しい。すなわち
H' の位数 ≤ H の位数
が成立し、これはH⊂H'なることから H=H'の場合に限って可能である。
以上から目的の等式 (*2) が証明された。 //
例1.
前章402節、及び前節で取り扱ったx3-2=0のガロア体について考
察する。
α= と置けば x3-2 の根はα,β=ωα , γ=ω2α (ω3=1)
となり K= R(α, β,γ) のガロア群は α , β , γ
のあらゆる置換から成る3次の対称群であることを既に説いた。
ガロア群 G には次の4つの部分群が存在する。 と置けば x3-2 の根はα,β=ωα , γ=ω2α (ω3=1)
となり K= R(α, β,γ) のガロア群は α , β , γ
のあらゆる置換から成る3次の対称群であることを既に説いた。
ガロア群 G には次の4つの部分群が存在する。
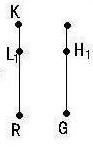 H1 = { 1 , (β , γ)}
H2 = {1,(β,γ)}
H3 = {1,(α,β)}
H4 = {1,(α,β,γ),(α,γ,β)}
勿論この他に単位元だけから成る単位群及び G その
ものが部分群であることは云うまでもない。
H1,H2,H3,H4にガロア理論の基本定理の意味で対応
する体をL1,L2,L3,L4 とする。
[K:L1] はそのガロア群 H1 の位数2に等しく、
[K:L1][L1:R ]=[K:R]
2[L1:R] = 6
すなわち[L1:R]=3であるが、
L1はK=R(α,β,γ)の中でH1の置換により不変な要素、
すなわち β,γ の交換により不変な要素の作る体であるから
L1⊂R(α)が成立し、
[L1:R]=3,[R(α):R]=3 から R(α)=L1が成立する。
同様にして
R(α)=L1,R(β)=L2,R(γ)=L3 H1 = { 1 , (β , γ)}
H2 = {1,(β,γ)}
H3 = {1,(α,β)}
H4 = {1,(α,β,γ),(α,γ,β)}
勿論この他に単位元だけから成る単位群及び G その
ものが部分群であることは云うまでもない。
H1,H2,H3,H4にガロア理論の基本定理の意味で対応
する体をL1,L2,L3,L4 とする。
[K:L1] はそのガロア群 H1 の位数2に等しく、
[K:L1][L1:R ]=[K:R]
2[L1:R] = 6
すなわち[L1:R]=3であるが、
L1はK=R(α,β,γ)の中でH1の置換により不変な要素、
すなわち β,γ の交換により不変な要素の作る体であるから
L1⊂R(α)が成立し、
[L1:R]=3,[R(α):R]=3 から R(α)=L1が成立する。
同様にして
R(α)=L1,R(β)=L2,R(γ)=L3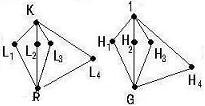 であることが分る。
L4 についてはH4の位数が
3 であるから
[K:L4]=3 , [L4:R]=2 である。
ω=β/α=(ω
であることが分る。
L4 についてはH4の位数が
3 であるから
[K:L4]=3 , [L4:R]=2 である。
ω=β/α=(ω )/ )/ は
( α,β,γ ) なる置換でγ/β=(ω2 は
( α,β,γ ) なる置換でγ/β=(ω2 )/ω )/ω =ω
に写るからω∈L4,R(ω)⊂L4である。
この関係と [L4:R]=2 , [R(ω):R]=2
から R(ω)=L4が導かれた。以上から
L1=R(α),L2=R(β),L3=R(γ),L4=R(ω)
( α= =ω
に写るからω∈L4,R(ω)⊂L4である。
この関係と [L4:R]=2 , [R(ω):R]=2
から R(ω)=L4が導かれた。以上から
L1=R(α),L2=R(β),L3=R(γ),L4=R(ω)
( α= ,β=ω ,β=ω ,γ=ω2 ,γ=ω2 )
なることが分った。
Gの単位群とG自身を部分群と考えたときこれに対応するK/R
の中間体はそれぞれ K 及び R である。 )
なることが分った。
Gの単位群とG自身を部分群と考えたときこれに対応するK/R
の中間体はそれぞれ K 及び R である。
|
以上から分るように部分体の重畳の模様は部分群の重畳の様子に反映
される。一方 部分体が重畳していることは一歩一歩方程式を解くこ
とに相当する。
ガロア群の部分群が可解群のような簡単な重畳を示すときには方程式
の根は簡単な演算を繰り返して求められることが明らかとなったが、
簡単な演算とはどのようなものであるかは後で述べる。
例2.
前節の例2で取り扱った x4 + 1 のガロア群の要素を
σ1(=1),σ2,σ3,σ4 とすれば、単位群1及び G 自身を除
けば G の部分群は次の3つである.
H1={1,σ2} , H2={1,σ3} , H3={1,σ4}
ここに σ2,σ3,σ4は ζを 1の8乗根としたとき
σ2:ζ⇒ζ3 , σ3:ζ⇒ζ5 , σ4:ζ⇒ζ7
なる置換であった。
部分群で不変な要素の作る体を求めるにはζの共役数の対称式を
まず試みに求めて見ることが有効で、簡単な場合にはこれで足り
ることが多い。
たとえばH1,H2,H3で不変な体 L1,L2,L3を求めるため、
ζ のこれらの体に関する共役数の対称式
1・ζ+σ2ζ , (1ζ)(σ2ζ)
1・ζ+σ3ζ , (1ζ)(σ3ζ)
1・ζ+σ4ζ , (1ζ)(σ4ζ)
を試みに求めれば
ζ=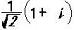 ( = ( =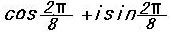 )
であるから
ζ+ζ3= )
であるから
ζ+ζ3=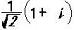 + +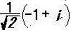 = = i , ζζ3 = -1
ζ+ζ5= i , ζζ3 = -1
ζ+ζ5=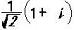 - -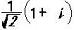 = 0 , ζζ5=-i
ζ+ζ7= = 0 , ζζ5=-i
ζ+ζ7=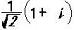 + +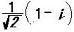 = = i , ζζ7=1
すなわち
R( i , ζζ7=1
すなわち
R( i,-1 )=R( i,-1 )=R( i )⊂L1
R(0,-1)=R(i)⊂L2
R( i )⊂L1
R(0,-1)=R(i)⊂L2
R( ,1)=R( ,1)=R( )⊂ L3
であるが、体の次数を考慮することにより )⊂ L3
であるが、体の次数を考慮することにより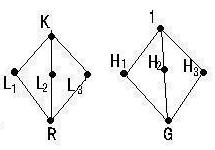 L1=R(
L1=R( i) , L2=R(i) , L3=R( i) , L2=R(i) , L3=R( )
が得られる。
この例では群と部分体の関係は
右図のようになる。 )
が得られる。
この例では群と部分体の関係は
右図のようになる。
|
|
 ることを示すには次の2つの式を証明すればよい。
(*1) Lh(L) = L
(*2) hL(H) = H
(*1) の式は H = h(L) , L(H) = L' と置いたとき
L'=L となることである。
L' は K の要素の中で H によって不変なものの集合であるが、HはLを
不変にする置換の集合であるからL⊂L' が成り立つ。
ることを示すには次の2つの式を証明すればよい。
(*1) Lh(L) = L
(*2) hL(H) = H
(*1) の式は H = h(L) , L(H) = L' と置いたとき
L'=L となることである。
L' は K の要素の中で H によって不変なものの集合であるが、HはLを
不変にする置換の集合であるからL⊂L' が成り立つ。
 次に K の要素 α が H で不変であったとする。
定理1.の証明の第1段によって K/L は正則拡大でそのガロア群は
丁度 H に一致する。
今もし αが Lの要素でなければ L(α)/Lの次数は1より大であり、
したがって恒等置換でないL(α)の L-同型対応が存在する。
定理1.によってこの対応は K/L のガロア置換に延長される。
すなわち K/L のガロア群である H の適当な置換によって、αは恒等
置換と異なる値に写る.これは矛盾であるからα∈Lでなければならない。
以上からL'⊂Lとなるから前に示した L⊂L'と合わせて L=L'=Lh(L)が
得られる。
次に K の要素 α が H で不変であったとする。
定理1.の証明の第1段によって K/L は正則拡大でそのガロア群は
丁度 H に一致する。
今もし αが Lの要素でなければ L(α)/Lの次数は1より大であり、
したがって恒等置換でないL(α)の L-同型対応が存在する。
定理1.によってこの対応は K/L のガロア置換に延長される。
すなわち K/L のガロア群である H の適当な置換によって、αは恒等
置換と異なる値に写る.これは矛盾であるからα∈Lでなければならない。
以上からL'⊂Lとなるから前に示した L⊂L'と合わせて L=L'=Lh(L)が
得られる。
 (*2)を証明する際にも先ずL(H)=L,h(L)=H'と置いたとき
H'⊃H なることが前と同様にして得られる。
H'は前にも述べたようにK/Lのガロア群であるからその
位数は [K:L] に等しい。
H の位数をhとしてその要素を σ1,σ2,・・・,σh
と置き、σ1=1 とすれば、K=L(θ)に対して
(*3) f(x)=(x-σ1θ)(x-σ2θ)・・・(x-σhθ)
は σ1θ = θ を根にもつ h 次の多項式である。
f(x) を x の冪に展開して
= xh-α1xh-1+ α2xh-2+・・・+(-1)hαh
と置けば
α1=σ1θ+σ2θ+・・・+σhθ
α2=(σ1θ)(σ2θ)+(σ1θ)(σ3θ)+・・・+(σh-1θ)(σhθ)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
αh=(σ1θ)(σ2θ)・・・(σhθ)
今 σ を H の任意の要素とすればたとえば σα1 は
(一般に σ により L の要素の積は像の積に写されること、
すなわち σ(αβ)=(σα)(σβ)なることに注意して)
σα2
=(σσ1θ)(σσ2θ)+(σσ1θ)(σσ3θ)+・・・+(σσh-1θ)(σσhθ)
同様にσαiはαiの式においてσjθをσσjθによって置き換えて
得られる. したがって
xh-σα1xh-1+ σα2xh-2+・・・・・・+(-1)hσαh
(*4) =(x-σσ1θ)(x-σσ2θ)・・・(x-σσhθ)
しかるに σ∈H であるから
σ1,σ2,・・・,σhとσσ1,σσ2,・・・,σσh は順序を除いて一致する。
したがって(*3)と(*4)は因数の順序を除いて一致し、それらの展開の
係数を比較して
σα1=α1,σα2=α2 , ・・・,σαh=αh
ここに σ は H の任意の要素であるから f(x) の係数 ±αi は L の
要素となり、θはh次のf(x)∈L[x]の根となることが証(明)された。
[K:L]はθの満足するL[x]における既約多項式の次数であるから
[K:L] ≤ h
一方 [K:L] は K/L のガロア群 H' の位数にも等しい。すなわち
H' の位数 ≤ H の位数
が成立し、これはH⊂H'なることから H=H'の場合に限って可能である。
以上から目的の等式 (*2) が証明された。 //
(*2)を証明する際にも先ずL(H)=L,h(L)=H'と置いたとき
H'⊃H なることが前と同様にして得られる。
H'は前にも述べたようにK/Lのガロア群であるからその
位数は [K:L] に等しい。
H の位数をhとしてその要素を σ1,σ2,・・・,σh
と置き、σ1=1 とすれば、K=L(θ)に対して
(*3) f(x)=(x-σ1θ)(x-σ2θ)・・・(x-σhθ)
は σ1θ = θ を根にもつ h 次の多項式である。
f(x) を x の冪に展開して
= xh-α1xh-1+ α2xh-2+・・・+(-1)hαh
と置けば
α1=σ1θ+σ2θ+・・・+σhθ
α2=(σ1θ)(σ2θ)+(σ1θ)(σ3θ)+・・・+(σh-1θ)(σhθ)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
αh=(σ1θ)(σ2θ)・・・(σhθ)
今 σ を H の任意の要素とすればたとえば σα1 は
(一般に σ により L の要素の積は像の積に写されること、
すなわち σ(αβ)=(σα)(σβ)なることに注意して)
σα2
=(σσ1θ)(σσ2θ)+(σσ1θ)(σσ3θ)+・・・+(σσh-1θ)(σσhθ)
同様にσαiはαiの式においてσjθをσσjθによって置き換えて
得られる. したがって
xh-σα1xh-1+ σα2xh-2+・・・・・・+(-1)hσαh
(*4) =(x-σσ1θ)(x-σσ2θ)・・・(x-σσhθ)
しかるに σ∈H であるから
σ1,σ2,・・・,σhとσσ1,σσ2,・・・,σσh は順序を除いて一致する。
したがって(*3)と(*4)は因数の順序を除いて一致し、それらの展開の
係数を比較して
σα1=α1,σα2=α2 , ・・・,σαh=αh
ここに σ は H の任意の要素であるから f(x) の係数 ±αi は L の
要素となり、θはh次のf(x)∈L[x]の根となることが証(明)された。
[K:L]はθの満足するL[x]における既約多項式の次数であるから
[K:L] ≤ h
一方 [K:L] は K/L のガロア群 H' の位数にも等しい。すなわち
H' の位数 ≤ H の位数
が成立し、これはH⊂H'なることから H=H'の場合に限って可能である。
以上から目的の等式 (*2) が証明された。 //
 と置けば x3-2 の根はα,β=ωα , γ=ω2α (ω3=1)
となり K= R(α, β,γ) のガロア群は α , β , γ
のあらゆる置換から成る3次の対称群であることを既に説いた。
ガロア群 G には次の4つの部分群が存在する。
と置けば x3-2 の根はα,β=ωα , γ=ω2α (ω3=1)
となり K= R(α, β,γ) のガロア群は α , β , γ
のあらゆる置換から成る3次の対称群であることを既に説いた。
ガロア群 G には次の4つの部分群が存在する。
 H1 = { 1 , (β , γ)}
H2 = {1,(β,γ)}
H3 = {1,(α,β)}
H4 = {1,(α,β,γ),(α,γ,β)}
勿論この他に単位元だけから成る単位群及び G その
ものが部分群であることは云うまでもない。
H1,H2,H3,H4にガロア理論の基本定理の意味で対応
する体をL1,L2,L3,L4 とする。
[K:L1] はそのガロア群 H1 の位数2に等しく、
[K:L1][L1:R ]=[K:R]
2[L1:R] = 6
すなわち[L1:R]=3であるが、
L1はK=R(α,β,γ)の中でH1の置換により不変な要素、
すなわち β,γ の交換により不変な要素の作る体であるから
L1⊂R(α)が成立し、
[L1:R]=3,[R(α):R]=3 から R(α)=L1が成立する。
同様にして
R(α)=L1,R(β)=L2,R(γ)=L3
H1 = { 1 , (β , γ)}
H2 = {1,(β,γ)}
H3 = {1,(α,β)}
H4 = {1,(α,β,γ),(α,γ,β)}
勿論この他に単位元だけから成る単位群及び G その
ものが部分群であることは云うまでもない。
H1,H2,H3,H4にガロア理論の基本定理の意味で対応
する体をL1,L2,L3,L4 とする。
[K:L1] はそのガロア群 H1 の位数2に等しく、
[K:L1][L1:R ]=[K:R]
2[L1:R] = 6
すなわち[L1:R]=3であるが、
L1はK=R(α,β,γ)の中でH1の置換により不変な要素、
すなわち β,γ の交換により不変な要素の作る体であるから
L1⊂R(α)が成立し、
[L1:R]=3,[R(α):R]=3 から R(α)=L1が成立する。
同様にして
R(α)=L1,R(β)=L2,R(γ)=L3 であることが分る。
L4 についてはH4の位数が
3 であるから
[K:L4]=3 , [L4:R]=2 である。
ω=β/α=(ω
であることが分る。
L4 についてはH4の位数が
3 であるから
[K:L4]=3 , [L4:R]=2 である。
ω=β/α=(ω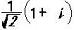 ( =
( =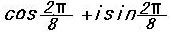 )
であるから
ζ+ζ3=
)
であるから
ζ+ζ3=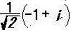 =
= i , ζζ3 = -1
ζ+ζ5=
i , ζζ3 = -1
ζ+ζ5=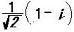 =
= L1=R(
L1=R(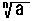 ( i=0,1,2,・・・,n-1 )
と表わすことができる。
ここに
( i=0,1,2,・・・,n-1 )
と表わすことができる。
ここに 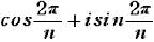 と置いた。
2、3、4次方程式の冪根による解法については既知のこととする.
冪根による代数方程式の解法を代数的な解法と云う。
尚正確には既約な素数次の2項方程式を解くこと及び4則の演算を
繰り返して求めることを代数的な解法ということにしよう。
ガロア群との関係を見るため次の定理を準備して、次節で代数的解法
のガロア理論による意味についてのべる。
と置いた。
2、3、4次方程式の冪根による解法については既知のこととする.
冪根による代数方程式の解法を代数的な解法と云う。
尚正確には既約な素数次の2項方程式を解くこと及び4則の演算を
繰り返して求めることを代数的な解法ということにしよう。
ガロア群との関係を見るため次の定理を準備して、次節で代数的解法
のガロア理論による意味についてのべる。
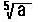 ( i = 0, 1, 2, 3, 4 )
で、仮定により ζ∈kであるから
k(αi) = k(ζi
( i = 0, 1, 2, 3, 4 )
で、仮定により ζ∈kであるから
k(αi) = k(ζi