さて、
Z の要素 a , b の組 (a,b) ( b ≠ 0 ) の全体 において、
同値(という関係)〜を次のように定義する。
(a,b) 〜 (c,d) とは ad = bc のことである
|
そうすればこの関係はつぎの 同値律の3つの法則 に従う。
・反射律 (a,b) 〜 (a,b)
・対称律 (a,b) 〜 (c,d) ならば (c,d) 〜 (a,b)
・推移律 (a,b) 〜 (c,d) かつ (c,d) 〜 (e,f)
ならば (a,b) 〜 (e,f)
証明について簡単に述べる。
・反射律:明らか。
・対称律:(a,b) 〜 (c,d) は ad = bc なること
(c,d) 〜 (a,b) は cb = da なること
に注意すれば正しいことが分る。
・推移律:仮定の2式により ad = bc , cf = de だから
第1式に f ,第2式に b を乗じて
adf = bcf , bcf = bde ∴ adf = bde
(c,d) において d ≠ 0 であるから、
簡約律( cf:101.(13))により d を約して
af = be ∴ (a,b) 〜 (e,f) //
証明自体は別段オモシロクも何ともありません。
( a , b ) は 分数 a/b = ab-1 に相当する概念を整数だけを
既知とし除法を未知であるものとして導入した記号である。また、
(a,b) 〜 (c,d) 即ち ad = bc は ab-1 = cd-1 を除法を用い
ないで表したものである。
以上によって有理数の概念は整数の除法を用いない性質だけで論
じられることが分った。
さらに進んで (a,b) , (c,d) の和、積をつぎのように定義する。
(a,b) + (c,d) = (ad + bc,bd)
(a,b)(c,d) = (ac,bd)
|
以上において 〜 の関係で同値な組の全体(すなわち1つの 類 )
は1つの有理数を表すものと考え、和と積を上のように定義すれば
次のようにして1つの 体 が得られていることが分る。
単位元の存在:
a,b が 0 でなければ (a,a) 〜 (b,b) なることが容易に分り、
(a,a)(b,d) = (ab,ad) 〜 (b,d) なることから
(a,a) の属する類を任意の類に乗じても始めの類に等しく
単位元の役をつとめる。
始めに述べた事実 (a,a) 〜 (b,b) は単位元の役をつと
める (a,a) , (b,b) , ・・・・・ 等が同値なものは区別しないもの
とすれば本質的には同じこと、
(即ち 類 C(a,a) = C(b,b) = ・・・)
したがってこのようにして単位元が1つだけ得られていること
を示す。
逆元 の 存在:
(0,b) + (c,d) = (bc,bd) 〜 (c,d) であるから
(0,b) の形の元は 零元 の役をつとめる。
したがって 逆元の存在( 202.(10) に相当する関係 ) は
(a,b) において a≠0 ならば
(a,b)(x,y) 〜 (c,c) のような x , y , c が存在する。”
と云い表される。そのためには
(a,b)(b,a) = (ab,ab)
なる関係を考慮に入れれば十分である。
少し難しくなってきたが・・・・・・より簡単に・・・、
( a , b )は単に2つの 数aとbを横に並べた組( ordered pair )
であり、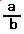 ,a/b, ,a/b,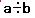 ,a割るbなどの分数を形を変えて表した
ものである・・・と思えば・・・分数や割り算と同じ仕組みであるから
少し分りやすくなるのではないだろうか・・・・・・。
このようにして得られた類 C( a , b ) を元とする体 P は、
整数環 Z と類似な構造をもつ部分集合 Z~ を含む。
何故かと云うと、
Z の元 a に ( ac , c ) の属する類 C( ac , c ) を対応
させればよい。
ここに c は Z の 任意の 0 でない元である。
このような対応を a →a~ = C( ac , c ) と表すとき、
次のような事実が成立する。 ,a割るbなどの分数を形を変えて表した
ものである・・・と思えば・・・分数や割り算と同じ仕組みであるから
少し分りやすくなるのではないだろうか・・・・・・。
このようにして得られた類 C( a , b ) を元とする体 P は、
整数環 Z と類似な構造をもつ部分集合 Z~ を含む。
何故かと云うと、
Z の元 a に ( ac , c ) の属する類 C( ac , c ) を対応
させればよい。
ここに c は Z の 任意の 0 でない元である。
このような対応を a →a~ = C( ac , c ) と表すとき、
次のような事実が成立する。
(11) C(ac,c)=C(ad,d)( 即ち(ac,c)〜(ad,d) )
(12) a~=b~ならばa=b
( 即ち異なるa,bが下図の左のように同じa~=b~に対応しないで
右のように対応する。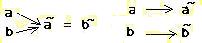 (13) a+b→a~+b~( (a+b)~=a~+b~と書いてもよい)
(14) ab→a~b~ ( (ab)~=a~b~と書いてもよい)
(13) a+b→a~+b~( (a+b)~=a~+b~と書いてもよい)
(14) ab→a~b~ ( (ab)~=a~b~と書いてもよい)
|
上の関係の中で (14) だけについて証明を与える。
abに対する像 a~b~は=C(abc,c) であり、
a~,b~ はそれぞれC(ac,c) , C(bc,c)であるから
(abc,c)〜(ac,c)(bc,c)を証明すればよい。
右辺は (acbc,cc)〜(acb,c)であるから左辺と同じ類に属する
こととなり、証明が終る。//
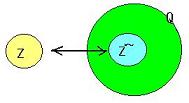
以上からZとZ~は所謂1対1の対応をなし、(13),(14)によって
加法、乗法に関する限り全く同じ構造を持つことが分った。
このことをZとZ~が同型
であると云ってZ Z~と表す。
以上の結果を図示すれば右図の
ようになる。 Z~と表す。
以上の結果を図示すれば右図の
ようになる。
|
|
数学では混同の恐れのない場合は類似の性質のもの
(とくに同型な代数系)を同じものと考えることが多い。
たとえば、黒板の上に書いた 3 と紙の上に
書かれた 3 とは異なるものであるが、数学的な
考察においては同じものと考えても混同を生ずる
ことはない。
このような意味で Z と Z~ は本質的には同じも
のと解釈すれば上の図は右の図のようになって、 |
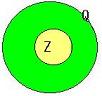 |
整数の環が1つの体の中に部分環として含まれることが分った。
以上の証明には整数環が整域であることだけの事実を用いている
ことに注目すれば つぎの定理が得られる。
定理:任意の整域を含む 体 が必ず存在する。
このような 体 のことを 始めの整域の 商体 (field of quotients)
という。
|
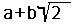 ( a ,b は整数 ) の全体 R は 環 である。
( a ,b は整数 ) の全体 R は 環 である。

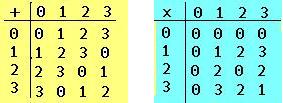
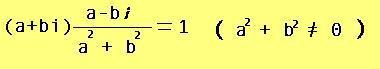 なることから分るからKは1つの体である。
K の要素で b = 0となるものの全体はとりも直さず有理数体Qであるから
Kは有理数体 Q の (iの添加による)拡大体であり、QはKの部分体である。
なることから分るからKは1つの体である。
K の要素で b = 0となるものの全体はとりも直さず有理数体Qであるから
Kは有理数体 Q の (iの添加による)拡大体であり、QはKの部分体である。
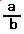 ,a/b,
,a/b,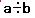 ,a割るbなどの分数を形を変えて表した
ものである・・・と思えば・・・分数や割り算と同じ仕組みであるから
少し分りやすくなるのではないだろうか・・・・・・。
このようにして得られた類 C( a , b ) を元とする体 P は、
整数環 Z と類似な構造をもつ部分集合 Z~ を含む。
何故かと云うと、
Z の元 a に ( ac , c ) の属する類 C( ac , c ) を対応
させればよい。
ここに c は Z の 任意の 0 でない元である。
このような対応を a →a~ = C( ac , c ) と表すとき、
次のような事実が成立する。
,a割るbなどの分数を形を変えて表した
ものである・・・と思えば・・・分数や割り算と同じ仕組みであるから
少し分りやすくなるのではないだろうか・・・・・・。
このようにして得られた類 C( a , b ) を元とする体 P は、
整数環 Z と類似な構造をもつ部分集合 Z~ を含む。
何故かと云うと、
Z の元 a に ( ac , c ) の属する類 C( ac , c ) を対応
させればよい。
ここに c は Z の 任意の 0 でない元である。
このような対応を a →a~ = C( ac , c ) と表すとき、
次のような事実が成立する。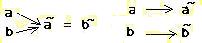 (13) a+b→a~+b~( (a+b)~=a~+b~と書いてもよい)
(14) ab→a~b~ ( (ab)~=a~b~と書いてもよい)
(13) a+b→a~+b~( (a+b)~=a~+b~と書いてもよい)
(14) ab→a~b~ ( (ab)~=a~b~と書いてもよい)
 Z~と表す。
以上の結果を図示すれば右図の
ようになる。
Z~と表す。
以上の結果を図示すれば右図の
ようになる。


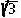 ( a , b は整数 ) の全体は環である
ことを示せ。また、
a + b
( a , b は整数 ) の全体は環である
ことを示せ。また、
a + b