今 φ(x) は体 k において既約な多項式であるとし、方程式 φ(x)=0
の根の1つを α とする。
また、k と α を含む最小の体を k(α) と表すことにする。
したがって、 k(α)は
kの元を係数にもつ多項式f(α),g(α)の比:f(α)/g(α) (*1)
の全体である。 体の復習 →
例1.
k を有理数の作る体とする。
φ(x)=x2+1 ならば i はφ(x)=0の根の1つである。
k(i) の任意の要素は有理数を係数に持つ多項式 f(i),g(i)
の比 f(i)/g(i) である。このとき、
f(x)=q(x)φ(x)+r(x)
( r(x)はφ(x)よりも低次の多項式 )
とおけば φ(i)=0 なることから
f(i)=q(i)φ(i)+r(i)=r(i)
が得られる。
r(x) は2次式 φ(x) よりも低次の多項式、すなわち
高々1次の多項式であるから
r(i)=a+bi ( a,b ∈k )
の形に書くことができる。同様にして、
g(i)=c+di ( c,d ∈ k )
と書くことができるから
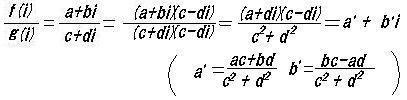 すなわち
k(i)は a+bi (a,b∈k) の全体からなる集合である。
すなわち
k(i)は a+bi (a,b∈k) の全体からなる集合である。
|
上の例で述べた事柄は一般の k(α) についても同じように成り立つ。
すなわち
定理1.
φ(x)を体 kの元を係数にもつ n次の既約多項式であり、
αをその1つの根とすれば k(α)の元はすべて
c0+c1α+c2α2+ ・・・ +cn-1αn-1
の形に唯1通りに表される。( ciはkの元である。)
|
定理2.→
証明
( 定理の前半 )
k(α)の元がc0+c1α+c2α2+・・・・・・ +cn-1αn-1の形であること・・・
k(α) の元はすべて (*1) すなわち f(α)/g(α) の形に書ける。
今 g(x) と φ(x) の最大公約数を d(x) とすれば、
d(x) は既約多項式φ(x) の約数であるから φ(x)または 1である。
もし d(x) = φ(x) ならば
g(x) = φ(x)h(x) したがって g(α) = φ(α)h(α) = 0
であるから g(α) は (*1) の分母にはなり得ない。
したがって g(x) と φ(x) の最大公約数 d(x) は 1 である。
更に、
「 g(x)とφ(x) の最大公約数が 1 ならば
a(x)g(x) + b(x)φ(x) = 1 (401-1→)
のような多項式 a(x),b(x) が存在する 」からxにαを代入して
a(α)g(α) = 1 ( b(α)φ(α) = 0 )
が得られる。
したがって k(α) の要素 f(α)/g(α) は
f(α)/g(α) = f(α)a(α) = h(α) ( 即ち α の多項式 )
の形に書くことができる。
つぎに h(x) を φ(x) で割った商を q(x)、剰余を r(x) とすれば
h(x) = q(x)φ(x) + r(x)
が成立し、
h(α) = q(α)φ(α) + r(α) = r(α)
なる等式が成り立つ。
r(x) は φ(x) より低次であるから k(α) の要素が
c0 + c1α + c2α2 + ・・・・・・ + cn-1αn-1 ・・・ (*2)
の形に表されることが分った。 //
|
( 定理の後半 )
・・・ 唯1通りであること
を証明するため k(α) の元が2通りに(*2)の形に書けたものとし
て、もう1つの表し方を
c'0 + c'1α + c'2α2 + ・・・・・・ + c'n-1αn-1 ・・・ (*3)
とすると、(*2)と(*3)は共にk(α)の1つの元を表しているのだから
b0 + b1α + b2α2 + ・・・・・・ + bn-1αn-1=0 (bi=ci-c'i)
なる関係式が得られる。
ψ(x) = b0 + b1x + b2x2 + ・・・・・・ + bn-1xn-1
とおけば α は ψ(x) の根であると同時に φ(x) の根でもある。
前と同様に ψ(x)とφ(x) の最大公約数は 1 またはφ(x) であるが、
ψ(x) は高々 n - 1次式だから n次の多項式φ(x)を約数に持つこと
はできない。
したがって ψ(x) と φ(x) の最大公約数は 1 となり、
a(x)ψ(x) + b(x)φ(x) = 1
のような多項式a(x),b(x) の存在が示され、x=αとおいて 0 = 1
なる矛盾に導かれる。 //
|
これで定理1が証明された。 //
上の証明を吟味することにより次の結果が得られる。
定理2.
φ(x)は体 kの要素を係数にもつ n次の既約多項式であり、
φ(α)=0 とする。このとき、
f(x) が k の元を係数に持つ多項式であるとすれば、
f(α)=0 なるための必要かつ十分な条件は
f(x)がφ(x)で割り切れることである。
|
証明 ( 所謂 因数定理であり、その証明である。)
f(x)がφ(x)で割りきれればf(α)=0なることは明らかである。
逆にf(α)=0であリ、かつf(x)がφ(x)で割り切れないならば
f(x),φ(x)の最大公約数は(φ(x)にはなり得ないから)1である。
したがって前定理の証明と同様に
a(x)f(x)+b(x)φ(x)=1
なる関係が得られ x=α とおくことにより 0=1
なる矛盾に導かれる。 //
|
k(α) のことを k に α を添加した体(拡大体)という。 定理1.→
一般に Kが kの拡大体であるとき、Kの元で kに関して1次独立
な元の個数の最大数 mを Kの kに関する次数といい、[K:k]と表す。
[K:k] = m なるとき Kの元 α1,α2,・・・・・・,αm で kに関して
1次独立なものを Kの kに関する底(基底 base) という。
αを n次の既約方程式φ(x)の根とすればkに関して1次独立な元は
定理1によって 1,α,α2,・・・・・・,αn-1 のn個だから [k(α):k]=n
である。すなわち、[k(α):k]はφ(x)の次数そのものである。
[これまでの要約と補足]
(1) n次の既約方程式φ(x)の1つの根αについて、
1, α, α2, ・・・・・・, αn-1
は1次独立であり、kの拡大体k(α)の元はすべて
c0+c1α+c2α2+ ・・・ +cn-1αn-1
の形(1次結合)に一意(1通り)に表される。
(2) k(α)のkに対する次数[k(α):k]はφ(x)の次数nに等しい.
すなわち、[k(α):k]=n .
(3) 1, α, α2, ・・・・・・, αn-1 が1次独立であるとは、
c0+c1α+c2α2+ ・・・ +cn-1αn-1=0 ⇔ c0=c1=c2= ・・・ =cn-1=0
が成り立つことをいう.
(4) 任意の n+1 個のk(α)の元が1次従属であるとは
1つの元が他のn個の元の1次結合で表されることをいう.
|
kにαを添加した体k(α) にさらに βを添加した体をk(α,β)と表す.
これは k の元を係数に持つ α,βの多項式の全体の作る体である.
同様にして k(α,β,γ)等を定義できて、つぎの関係になる.
k⊂k(α)⊂k(α,β)⊂k(α,β,γ)⊂・・・ 401-2→
これに対してk(α)のように唯1つの元を添加した体のことを
単純拡大体といって区別する.このとき、αをk(α)=Kの生成元 という.
402th6→
次の用語の意味を上の文章の中から読み取って考えよう.
体:既約多項式:拡大体:1次独立:1次従属:底(base):
単純拡大体:次数:生成元:
定理3.
k⊂K⊂L なる3つの体があり、Lのkに対して
1次独立な元の個数が有限ならば次の公式が成り立つ.
[L:k] = [L:K][K:k].
( このとき KをL,kの中間体という.501→ )
|
証明: ( 一見大掛かりな証明だが、分りやすいと思う. )
Lの kに対する1次独立な元の個数が有限なとき、[L:k]<∞
と表す.
Kは Lの部分体であるから Kの元の kに関して1次独立なもの
の個数(次数)[K:k]は[L:k]を越えないから [K:k]<∞である.
次に Lの元で Kに関して1次独立な元は、kの元が
Kに含まれることに注意すれば、kに関しても1次独立である.
したがって [L:K] ≤ [L:k] < ∞である.
さて [K:k]=m , [L:K]=n はいずれも有限であるから
Kの kに対する底 α1,α2,・・・・・・,αm および
Lの Kに関する底 β1,β2,・・・・・・,βn が存在する.
このとき mn 個の元 αiβj ( 1≤i< m,1≤j < n )
が Lの kに関する底であることを示せば定理が証明された
ことになる.
そのためには Lの任意の元が kの元を係数にもつαiβj
の1次結合となること 及び αiβjが kに関して1次独立
であることを示せばよい.
Lの Kに関する底が βjであることから Lの任意の元は
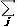 ujβj ( uj ∈K )
の形に唯1通りに表わされる.
ここに Kの元 ujは Kのkに関する底αiによって1通りに
uj = ujβj ( uj ∈K )
の形に唯1通りに表わされる.
ここに Kの元 ujは Kのkに関する底αiによって1通りに
uj = 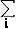 cijαi (cij∈k)
の形に表わされる.
以上の2つの結果を組み合わせてLの元は cijαi (cij∈k)
の形に表わされる.
以上の2つの結果を組み合わせてLの元は
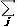 ujβj= ujβj=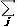 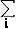 cijαiβj= cijαiβj=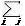 cijαiβj
の形に表わすことが分った.
次に αiβj が1次独立なことを示すため cijαiβj
の形に表わすことが分った.
次に αiβj が1次独立なことを示すため
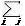 cijαiβj = 0 ( cij∈k ) (*1)
であると仮定すれば、 cijαiβj = 0 ( cij∈k ) (*1)
であると仮定すれば、
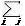 cijαiβj= cijαiβj=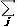 ujβj= 0 ( uj= ujβj= 0 ( uj=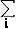 cijαi∈K )
βjがLのKに関する底であり、したがってKに関して1次独立
であることから
uj = cijαi∈K )
βjがLのKに関する底であり、したがってKに関して1次独立
であることから
uj = 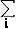 cijαi = 0
αiはKのkに関する底であり、したがってkに関して1次独立
であることから cij = 0 (*2)
すなわち (*1) から (*2) が結論されて
αiβj が k に関して1次独立
なることが証明された. // cijαi = 0
αiはKのkに関する底であり、したがってkに関して1次独立
であることから cij = 0 (*2)
すなわち (*1) から (*2) が結論されて
αiβj が k に関して1次独立
なることが証明された. //
|
例2.kを有理数体とし、kにおいて既約な代数方程式
x4 - 2x2 + 9 = 0
の根の1つをθ= +i とすれば k(θ)のkに関する
1つの底は定理1.から 1, θ, θ2, θ3 であり、
[k(θ),k]=4 である. +i とすれば k(θ)のkに関する
1つの底は定理1.から 1, θ, θ2, θ3 であり、
[k(θ),k]=4 である.
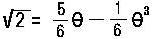 , , 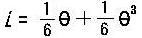 であるから
であるから  ,i はk(θ)の元である。 (401-3 →) ,i はk(θ)の元である。 (401-3 →)
 は x2 - 2 = 0 の根であるから
k( は x2 - 2 = 0 の根であるから
k( ) = K は k に関して2次の体である.
また i は実数からなる体 k( ) = K は k に関して2次の体である.
また i は実数からなる体 k( )の元とは成り得ず、
一方 x2+1=0 の根であるからK(i)=k( )の元とは成り得ず、
一方 x2+1=0 の根であるからK(i)=k( ,i)=L はKに
関して2次の体である。 ,i)=L はKに
関して2次の体である。 上の定理から [L:k]=[L:K][K:k]=2・2=4 であり,
また L=k(
上の定理から [L:k]=[L:K][K:k]=2・2=4 であり,
また L=k( ,i)⊂ k(θ)
から図のような関係が得られ
4=[k(θ):k]=[k(θ):L][L:k]=[k(θ):L]・4
なる等式により [k(θ):L] = 1
すなわち 実は k(θ)=k( ,i)⊂ k(θ)
から図のような関係が得られ
4=[k(θ):k]=[k(θ):L][L:k]=[k(θ):L]・4
なる等式により [k(θ):L] = 1
すなわち 実は k(θ)=k( ,i)=L なることが分る.
以上から ,i)=L なることが分る.
以上から
 と i の添加による k の拡大体 L は k(θ)そのもの
である.
すなわち、
k に関して4次の体 k(θ) が2次の体 L/K , K/k を
積み重ねることにより得られることが分った。例3.→
( K/k は kの拡大体としてのK を表すものとする. )
ただし、4次の体が常に2次の体を積み重ねて得られる
とは限らない. 402th6→ と i の添加による k の拡大体 L は k(θ)そのもの
である.
すなわち、
k に関して4次の体 k(θ) が2次の体 L/K , K/k を
積み重ねることにより得られることが分った。例3.→
( K/k は kの拡大体としてのK を表すものとする. )
ただし、4次の体が常に2次の体を積み重ねて得られる
とは限らない. 402th6→
|
定理4.
φ(x) を k の元を係数にもつ既約多項式、
α,βをφ(x) の2根とすれば k(α),k(β)は
kの元をそれ自身に対応させるような対応
(kの元を動かさない対応ともいう)
において同型( k(α) k(β) )である.
例4→ 401-6→ k(β) )である.
例4→ 401-6→
|
[ 402の単純拡大体へ続く準備である。]
証明:k(α)とk(β) が適当な対応により定理で述べたような
同型対応をすることを示す.
kの元を動かさない対応 σ:k(α)→k(β) によって
k(α)の元 f(α)=a0+a1α+a2α2+・・・+an-1αn-1
( a0,a1,・・・,an-1∈k )
が k(β)の元 f(β)=a0+a1β+a2β2+・・・+an-1βn-1
に写されたとする.すなわち、σ(f(α))=f(β) とする.
このとき、σが体k上の同型対応であることを示せばよい.
u=a0+a1α+a2α2+・・・+an-1αn-1
v=b0+b1α+a2α2+・・・+bn-1αn-1 (ai,bi∈k) とおくと、
先ず、σ(u+v)=σ(u)+σ(v) であることは直ちに分る.
つぎに、g(x)=a0+a1x+a2x2+・・・+an-1xn-1
h(x)=b0+b1x+b2x2+・・・+bn-1xn-1
とおくと、
σ(u)=g(β) , σ(v)=h(β) ・・・①
である.
そこで、g(x)h(x)=s(x)φ(x)+r(x) , degr(x) < n
とおくと、α,βはφ(x) の2根 だから
uv=g(α)h(α)=s(α)φ(α)+r(α)=r(α)
∴ σ(uv)=σ(r(α))=r(β)=g(β)h(β) ・・・②
①、②より、σ(uv)=r(β)=g(β)hβ)=σ(u)σ(v)
が成り立つ.
また、
kの元cにはそれ自身が対応すること、すなわち c→c なる
ことは明らかである(kの元はαの0次の多項式と考えられ
ることに注意).
以上によってσは体k上の同型対応である. //
|
上の定理で述べたように k(α) と k(β) が
k の元をそれ自身に対応させる対応(つまりkの元を動かさない
対応)で同型であることをkに関して同値であるといい、そのよ
うな対応のことをk-同型対応 という. 402定理8→ 501→
例3.
k を有理数体とするとき
k(i)/kは2次の体で、iの満足する既約多項式は
φ(x)=x2+1=0 例2.→
であるから、
f(x)∈k[x] なるとき f(i) → f(-i)
によって k(i),k(-i)はkに関して同値 である.
k(i) の元は前に述べたようにすべて a+bi ( a,b∈k )
の形に書くことができるから k(i),k(-i)の間の同型対応は
各数を共役複素数に写す同型対応:
a+bi → a-bi
であると考えてよい. (このとき、kの元a,b は動かない.)
|
この例では実は k(i)=k(-i)であるから上の同型対応は
k(i)自身の中での元iの置換である.
このように1つの代数系の自分自身の内部での同型対応の
ことを自己同型対応という. 402例1(1)→ 501→
例4.
k を有理数体とすれば φ(x) = x3 - 2 は kにおいて
既約な多項式で、その根は
α= , β=ω , β=ω , γ=ω2 , γ=ω2 ( ω:ω3=1,ω≠1 )
である。 定理4.によって k(α),k(β),k(γ) は kに
関して同値である.
β は虚数であるから、実数ばかりから成る体 k(α)
の元ではあり得ない.
したがって、
k(α)からk(β)への同型対応は自己同型対応ではない.
k(β)からk(γ)への同型対応は自己同型対応である.
( ω:ω3=1,ω≠1 )
である。 定理4.によって k(α),k(β),k(γ) は kに
関して同値である.
β は虚数であるから、実数ばかりから成る体 k(α)
の元ではあり得ない.
したがって、
k(α)からk(β)への同型対応は自己同型対応ではない.
k(β)からk(γ)への同型対応は自己同型対応である.
|
一般に φ(x)が k[x]の既約な多項式であり、その根が
α,β,γ,・・・・・・ であるとき、k(α),k(β),k(γ),・・・
を kに関して互いに共役な体という.
また、それらの元 : f(α),f(β),f(γ),・・・
も kに関して互いに共役な元という.
共役な体はφ(x)の次数だけ存在するが、例3でもみたよう
に異なる記号で表された共役な体が一致することがある
(自己同型対応)ことに注意しなければならない。
402th8→ 402例1(2)→ 501→
次の用語の意味を上の文章の中から読み取って考えよう.
mn個の元:2次の体:既約多項式:同型:多項式環:
kに関して同値:k-同型対応:自己同型(対応):
共役な体、共役な元:共役な体の一致:中間体:
|