101-1 a + c = b + c の両辺に -c を加えて
(a + c) + (-c) = (b + c) + (-c)
(2)により a + (c + (-c)) = b + (c + (-c))
(8)により a + 0 = b + 0
(6)により a = b //
101-2 (4) , (5) , (9) , (8)
戻る
102-1 (1) m|a , m|b より a = hm , b = km と表される( h , k は整数 )。
ゆえに a ± b = hm ± km = ( h + k )m ゆえに m|( a ± b ) //
(2) m|a より a = hm, ab= (hm)b= h(mb)= h(bm)= (hb)m ゆえに m|ab //
(3) a|b , b|c より b = am , c = bn と表される( m , n は整数 )
ゆえに c = bn = (am)n = a(mn) ゆえに a|c //
戻る
102-2 |ab| = |a||b|a = mq + r とすると a - a = 0 = m・0 ゆえに a ≡ b //
a ≡ b ( mod m ) より a - b = km
ゆえに b - a = -km = (-k)m ゆえに b ≡ a ( mod m ) //
a ≡ b ( mod m ) より a - b = km , b ≡ c ( mod m ) より b - c = hm
ゆえに a - c = a - b + b - c = ( a - b ) + ( b - c )
= km - hm = ( k - h )m
ゆえに a ≡ c ( mod m ) //
戻る
103-1 (4) |ab| = |a||b|
a ≥ 0 , b ≥ 0 のとき ab ≥ 0
だから |a| = a , |b| = b , |ab| = ab
ゆえに |ab| = |a||b|
a < 0 , b ≥ 0 のとき ab ≤ 0
だから |a| = -a , |b| = b , |ab| = -ab = (-a)b
ゆえに |ab| = -ab = (-a)b
ゆえに |ab| = |a||b|
a ≥ 0 , b < 0のとき ab ≤ 0
だから |a| = a , |b| = -b , |ab| = -ab = a(-b)
ゆえに |ab| = |a||b|
a < 0 , b < 0 のとき ab > 0
だから |a| = -a , |b| = -b , |ab| = ab = (-a)(-b)
ゆえに |ab| = |a||b|
ゆえに |ab| = |a||b| は成り立つ //
(5) 略 戻る
103-2 a > 0 ならば a2 > 0・a = 0
a < 0 ならば -a > 0 ゆえに a(-a) < 0・(-a) = 0 ゆえに -a2 < 0
ゆえに a2 > 0 //
この証明から、|a|2 = a2 が成り立つことが分る。これを公式とする。
戻る
103-3 (1) 上の公式を用いる。
a2+b2-2|ab|=|a|2-2|a||b|+|b|2=(|a|-|b|)2 ≥0 //
(2) a2+ab+b2 = (a+b/2)2+(3/4)・b2≥0 //
戻る
201-1 3n ( n は整数 ) の形の数は (1)〜(7) を満たす。ゆえに 環 である。
ただし、1 は 3 の倍数ではないから (8) をみたす e とはなり得ない。
よって整域 ではない。// 戻る
201-2 a2 = a と(8)により aa = ea ∴ aa - ea = ( a - e )a = 0
(9) により a - e = 0 ∨ a = 0 ∴ a = e ∨ a = 0 // 戻る
203-1 a+b ( a,bは有理数 ) について
(a+b ( a,bは有理数 ) について
(a+b )+(0+0 )+(0+0 )=a+b )=a+b , (a+b , (a+b )+(-a-b )+(-a-b )=0+0 )=0+0 すなわち 0+0
すなわち 0+0 は零元であり、a+b は零元であり、a+b (a,bは有理数)の全体は環である。
また、
(a+b (a,bは有理数)の全体は環である。
また、
(a+b )×<1+0 )×<1+0 )=a+b )=a+b すなわち 1+0 すなわち 1+0 は単位元であり
(a+b は単位元であり
(a+b )×(x+y )×(x+y )=1+0 )=1+0 とおくと、x=a/(a2-3b2) , y=-b/(a2-3b2)
すなわち x+y とおくと、x=a/(a2-3b2) , y=-b/(a2-3b2)
すなわち x+y はa+b はa+b の逆元であり、
a+b の逆元であり、
a+b (a,bは有理数)の全体は体である。
戻る
203-2 (a,bは有理数)の全体は体である。
戻る
203-2
 戻る
203-3 任意のa,bε;Qについて(a,b)のぜんたいをPとし、Pのなかでは
2つの演算 (a,b)+(c,d)=(a+c,b+d) ,
(a,b)・(c,d)=(ac-bd,ad+bc) が定義されている。
Pの任意の元をp=(a,b) , q=(c,d) , r=(e,f)としてPが体の
条件をみたすかについて簡単に検証する。
(1) p+(q+r)=(p+q)+r
(2) p+q=q+p
(3) p+O=p O は O=(0,0) である。
(4) p+x=0 x は x=-p=(-a,-b) である。
(5) p(qr)=(a,b)((c,d)(e,f))=(a,b)(ce-df,cf+de)
=(a(ce-df)-b(cf+de),a(cf+de)-b(ce-df))
=(ace-adf-bcf-bde,acf+ade-bce+bdf)・・・・・・(*1)
(pq)r=((a,b)(c,d))(e,f)=(ac-bd,ad+bc)(e,f)
=((ac-bd)e-(ad+bc)f,(ac-bd)f+(ad+bc)e)
=(ace-bde-adf-bcf,acf-bdf+ade+bce)
=(ace-adf-bcf-bde,acf+ade-bce+bdf)・・・・・・(*2)
(*1),(*2)より p(qr)=(pq)r は成り立つ。//
(6) pq=(a,b)(c,d)=(ac-bd,ad+bc)
qp=(c,d)(a,b)=(ca-bd,cb+da)=(ac-bd,ad+bc) ∴pq=qp //
(7) p(q+r)=pq+pr,(q+r)p=qp+rp 略
(8) 単位元はε=(1,0) である。
(9) pq=(a,b)(c,d)=(ac-bd,ad+bc)=0 ならば ac-bd=0,ad+bc=0
∴(a2+b2)(c2+d2)=(ac-bd)2+(ad+bc)2=0+0=0
∴a2+b2=0 or c2+d2=0
∴p=0 or q=0 //
(10) (a,b)(x,y)=(ax-by,ay+bx)=(1,0) より ax-by=1 , ay+bx=0
これを解いて、x=a/(a2+b2),y=-b/(a2+b2)
x,y は有理数である。ゆえにp( ≠0 )の逆元は存在する。
よって P はこの2つの演算において体をなす。 戻る
203-4 a+bi→a-bi , c+di→c-di とする。このとき、
(a+bi)+(c+di)=a+c+(b+d)i , (a-bi)+(c-di)=a+c-(b+d)i)
∴a+c+(b+d)i)→a+c-(b+d)i)
(a+bi)・(c+di)=ac-bd+(ad+bc)i , (a-bi)・(c-di)=ac-bd-(ad+bc)i
∴ac-bd+(ad+bc)i→ac-bd-(ad+bc)i
よって a+bi→a-biなる対応は2つの演算 + , ・について
同型対応である。
戻る
301-1 右表の通り。単位元は b 戻る
203-3 任意のa,bε;Qについて(a,b)のぜんたいをPとし、Pのなかでは
2つの演算 (a,b)+(c,d)=(a+c,b+d) ,
(a,b)・(c,d)=(ac-bd,ad+bc) が定義されている。
Pの任意の元をp=(a,b) , q=(c,d) , r=(e,f)としてPが体の
条件をみたすかについて簡単に検証する。
(1) p+(q+r)=(p+q)+r
(2) p+q=q+p
(3) p+O=p O は O=(0,0) である。
(4) p+x=0 x は x=-p=(-a,-b) である。
(5) p(qr)=(a,b)((c,d)(e,f))=(a,b)(ce-df,cf+de)
=(a(ce-df)-b(cf+de),a(cf+de)-b(ce-df))
=(ace-adf-bcf-bde,acf+ade-bce+bdf)・・・・・・(*1)
(pq)r=((a,b)(c,d))(e,f)=(ac-bd,ad+bc)(e,f)
=((ac-bd)e-(ad+bc)f,(ac-bd)f+(ad+bc)e)
=(ace-bde-adf-bcf,acf-bdf+ade+bce)
=(ace-adf-bcf-bde,acf+ade-bce+bdf)・・・・・・(*2)
(*1),(*2)より p(qr)=(pq)r は成り立つ。//
(6) pq=(a,b)(c,d)=(ac-bd,ad+bc)
qp=(c,d)(a,b)=(ca-bd,cb+da)=(ac-bd,ad+bc) ∴pq=qp //
(7) p(q+r)=pq+pr,(q+r)p=qp+rp 略
(8) 単位元はε=(1,0) である。
(9) pq=(a,b)(c,d)=(ac-bd,ad+bc)=0 ならば ac-bd=0,ad+bc=0
∴(a2+b2)(c2+d2)=(ac-bd)2+(ad+bc)2=0+0=0
∴a2+b2=0 or c2+d2=0
∴p=0 or q=0 //
(10) (a,b)(x,y)=(ax-by,ay+bx)=(1,0) より ax-by=1 , ay+bx=0
これを解いて、x=a/(a2+b2),y=-b/(a2+b2)
x,y は有理数である。ゆえにp( ≠0 )の逆元は存在する。
よって P はこの2つの演算において体をなす。 戻る
203-4 a+bi→a-bi , c+di→c-di とする。このとき、
(a+bi)+(c+di)=a+c+(b+d)i , (a-bi)+(c-di)=a+c-(b+d)i)
∴a+c+(b+d)i)→a+c-(b+d)i)
(a+bi)・(c+di)=ac-bd+(ad+bc)i , (a-bi)・(c-di)=ac-bd-(ad+bc)i
∴ac-bd+(ad+bc)i→ac-bd-(ad+bc)i
よって a+bi→a-biなる対応は2つの演算 + , ・について
同型対応である。
戻る
301-1 右表の通り。単位元は b 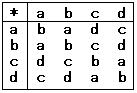 301-2
301-2
 正方形を移動して頂点1234がABCDになったことを(ABCD)
とかくことにすると、その移動はつぎの8個になる。
e=(1234) , a=(2341) , b=(3412) , c=(4123)
p=(24) , q=(13) , r=(14)(23) , s=(12)(34)
これらの移動について、乗積表(群表)をつくる。
例:ab=(2341)(3412)=(4123)=c 以下略。 戻る
301-3 (ab)(b-1a-1)=a(b(b-1a-1))=a((bb-1)a-1)=a(ea-1)
=a(a-1)=aa-1 = e
同様にして (b-1a-1)(ab) = e // 戻る
301-4 すべての群表の形を書き下してみる。有限個(数個)の群表だから
すぐ終る。
どの群表も左対角線に関して対称であることを確かめればよい。
戻る
302-1 a≡a(mod H)
a≡b(mod H) ⇒ aH=bH ∴bH=aH ∴ b≡a(mod H)
a≡b(mod H),b≡c(mod H) ⇒ aH=bH,bH=cH∴aH=cH∴a≡c(mod H)
ゆえに同値律をみたす。 //
a∈H ⇒ ca∈aH
b∈H ⇒ cb∈bH
a≡b(mod H) だから aH = bH = H ∴ ca∈H , cb∈H
∴ ca≡cb(modH) //
戻る
302-2 a の逆元が x , y ( x キ y ) の2個あるとすると、
ax = xa = e (1)
ay = ya = e (2)
だから
y=ye=y(ax) = (ya)x = ex = x
ゆえに y = x となって矛盾。
したがって対応 a→a-1 は1対1である。
たとえば
1 , -1 からなる乗法の群 G = { 1 , -1 } を考える。
G における対応f: 1→-1 , -1→1
では 1・(-1) = -1 しかるに f(1)f(-1) = (-1)・1 = -1 キ f(-1)
ゆえに G における対応 f は同型対応ではない。// 戻る
303-0 正方形を移動して頂点1234がABCDになったことを(ABCD)
とかくことにすると、その移動はつぎの8個になる。
e=(1234) , a=(2341) , b=(3412) , c=(4123)
p=(24) , q=(13) , r=(14)(23) , s=(12)(34)
これらの移動について、乗積表(群表)をつくる。
例:ab=(2341)(3412)=(4123)=c 以下略。 戻る
301-3 (ab)(b-1a-1)=a(b(b-1a-1))=a((bb-1)a-1)=a(ea-1)
=a(a-1)=aa-1 = e
同様にして (b-1a-1)(ab) = e // 戻る
301-4 すべての群表の形を書き下してみる。有限個(数個)の群表だから
すぐ終る。
どの群表も左対角線に関して対称であることを確かめればよい。
戻る
302-1 a≡a(mod H)
a≡b(mod H) ⇒ aH=bH ∴bH=aH ∴ b≡a(mod H)
a≡b(mod H),b≡c(mod H) ⇒ aH=bH,bH=cH∴aH=cH∴a≡c(mod H)
ゆえに同値律をみたす。 //
a∈H ⇒ ca∈aH
b∈H ⇒ cb∈bH
a≡b(mod H) だから aH = bH = H ∴ ca∈H , cb∈H
∴ ca≡cb(modH) //
戻る
302-2 a の逆元が x , y ( x キ y ) の2個あるとすると、
ax = xa = e (1)
ay = ya = e (2)
だから
y=ye=y(ax) = (ya)x = ex = x
ゆえに y = x となって矛盾。
したがって対応 a→a-1 は1対1である。
たとえば
1 , -1 からなる乗法の群 G = { 1 , -1 } を考える。
G における対応f: 1→-1 , -1→1
では 1・(-1) = -1 しかるに f(1)f(-1) = (-1)・1 = -1 キ f(-1)
ゆえに G における対応 f は同型対応ではない。// 戻る
303-0  (1) (123) (132) (23) (13) (12) //戻る
303-1 S3の元は n!=6個 であるが、S3の部分群(すなわち演算において
閉じていて逆元の存在する集合)は次の4個である。
{1,(12)}, {1,(13)}, {1,(23)}, {1,(123),(132)} // 戻る
303-2 前問のとおりS3の部分群は4個ある。そのうち {1,(123),(132)}は
偶置換だけからなる交代群である。
3次の交代群A3の元の個数は
3・2・1/2=3 すなわち 1, (123), (132) の3個 // 戻る
303-3 4次の対称群 S4の元をそれぞれを互換の積に分解しながら書くと・・・
・(1234)=(1) ・(3124)=(132)=(13)(12)
(1243)=(34) (3142)=(1342)=(13)(14)(12)
(1324)=(23) ・(3241)=(134)=(13)(14)
・(1342)=(234)=(23)(24) (3214)=(13)
・(1423)=(243)=(24)(23) ・(3412)=(13)(24)
(1432)=(24) (3421)=(1324)=(13)(12)(14)
(2134)=(12) (4123)=(1432)=(14)(13)(12)
・(2143)=(12)(34) ・(4132)=(142)=(14)(12)
・(2314)=(123)=(12)(13) ・(4213)=(143)=(14)(13)
(2341)=(1234)=(12)(13)(14) (4231)=(14)
(2413)=(1243)=(12)(14)(13) (4312)=(1423)=(14)(12)(13)
・(2431)=(124)=(12)(14) ・(4321)=(14)(23)
4次の交代群A4の元は偶置換だから上記の・をつけた4・3・2・1/2=12個
である。すなわち、
A4={ (1), (123), (132), (124), (142), (134), (143),
(234), (243), (12)(34), (13)(24), (14)(23) } // 戻る
303-4
(1) (123) (132) (23) (13) (12) //戻る
303-1 S3の元は n!=6個 であるが、S3の部分群(すなわち演算において
閉じていて逆元の存在する集合)は次の4個である。
{1,(12)}, {1,(13)}, {1,(23)}, {1,(123),(132)} // 戻る
303-2 前問のとおりS3の部分群は4個ある。そのうち {1,(123),(132)}は
偶置換だけからなる交代群である。
3次の交代群A3の元の個数は
3・2・1/2=3 すなわち 1, (123), (132) の3個 // 戻る
303-3 4次の対称群 S4の元をそれぞれを互換の積に分解しながら書くと・・・
・(1234)=(1) ・(3124)=(132)=(13)(12)
(1243)=(34) (3142)=(1342)=(13)(14)(12)
(1324)=(23) ・(3241)=(134)=(13)(14)
・(1342)=(234)=(23)(24) (3214)=(13)
・(1423)=(243)=(24)(23) ・(3412)=(13)(24)
(1432)=(24) (3421)=(1324)=(13)(12)(14)
(2134)=(12) (4123)=(1432)=(14)(13)(12)
・(2143)=(12)(34) ・(4132)=(142)=(14)(12)
・(2314)=(123)=(12)(13) ・(4213)=(143)=(14)(13)
(2341)=(1234)=(12)(13)(14) (4231)=(14)
(2413)=(1243)=(12)(14)(13) (4312)=(1423)=(14)(12)(13)
・(2431)=(124)=(12)(14) ・(4321)=(14)(23)
4次の交代群A4の元は偶置換だから上記の・をつけた4・3・2・1/2=12個
である。すなわち、
A4={ (1), (123), (132), (124), (142), (134), (143),
(234), (243), (12)(34), (13)(24), (14)(23) } // 戻る
303-4 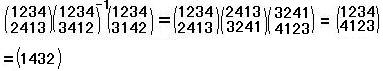 // 戻る
303-5 6,4,3 の最小公倍数=12 // 戻る
303-6 // 戻る
303-5 6,4,3 の最小公倍数=12 // 戻る
303-6
 A4の部分群:K={(1),(12)(34),(13)(24),(14)(23)} について、
e=(1),p=(12)(34),q=(13)(24),r=(14)(23)
とおいたときのKの乗積表を左に示す。
左対角線を軸に対称となり、アーベル群である。
また、Kの中に位数2の部分群:{e,p},{e,q},{e,r}
があることも分る。
戻る
練習1:(12)→(12)(12)(12)=(12) は明らか。
(13)→(12)(13)(12)=(123)(12)=(213)=(132)=(23)
(23)→(12)(23)(12)=(12)((12)(13)(12))(12) (上の結果を用いた)
=((12)(12))(13)((12)(12))=(13)
(123)→(12)(123)(12)=(12)((12)(13))(12)
=((12)(12))(13)(12)=(13)(12)=(132)
(132)→(12)(132)(12)=(12)((13)(12))(12)
=((12)(13))(12)(12)=(12)(13)=(123) //
すなわち、S3の内部自己同型は全単射であるから同型対応であり、
S3と一致する。
したがって、後で述べることになるがS3は正規部分群である。
戻る
練習2:f:G → G'(準同型対応) のもとで H:Gの部分群→f(H):G'の部分群
を示したい。
それは即ち
仮定:h1 , h2∈H ⇒ h1・h2-1∈H (1)
結論:h'1 , h'2∈f(H) ⇒ h'1・h'2-1∈f(H) (2)
を示すことである。
(2) の仮定より始めて h'1 , h'2∈f(H) とすると
h'1=f(h1) , h2'=f(h2) ( h1 , h2∈H )
と書ける。
準同型写像の性質から
h'1・h'2-1=f(h1)・f(h2)-1=f(h1)・f(h2-1)=f(h1・h2-1)∈f(H)
これで (2) が示せた。 //戻る
練習3:S3={1,(12),(13),(23),(123),(132)} について、
交代群A3={1,(123),(132)}の (23)による内部同型置換 を求めると、
(23)1(23)=1
(23)(123)(23)=(23)(231)(23)=(23)(23)(21)(23)
=(21)(23)=(213)=(132)
(23)(132)(23)=(23)(213)(23)=(23)(21)(23)(23)
=(23)(21)=(231)=(123)
同様に
S3 の任意の元a による1,(123),(132)の内部同型置換は 1,(123),(132)に
1対1で対応する。すなわち、
S3の任意の元aについてa-1A3a=A3が成り立つからA3は正規部分群である。//
また、S4 の元例えば(12)による交代群A4の内部同型置換をすると、
(12)A4(12)=A4が成り立つ。何故ならば、
A4は偶置換の集合だからS4の任意の元、例えば(12)
に対してA4(12)、(12)A4は共に奇置換の集合であり、
A4(12)∪A4=(12)A4∪A4=S4 , A4(12)∩A4=(12)A4∩A4=φ
∴A4(12)=(12)A4 ∴(12)A4(12)=(12)(12)A4=A4
すなわち、
S4の元aについて a-1A4a=A4 だから A4 は正規部分群である。 // 戻る
練習4:f が全射という意味は: ∀g'∈G',∃g∈G ; f(g)=g'であることをいう。
( G'の任意(arbitrary)の元g'に対して f(g)=g'をみたすGの元g
が存在する(exist) ということ。)
練習2.でf(H)がG'の部分群であることは示されているから、あとは
f(H)が正規部分群の条件をみたしていることを示せばよい。
すなわち
仮定:g∈G,h∈H ⇒ g-1hg∈H (1)
結論:g'∈G',h'∈H ⇒ g'-1・h'・g'∈f(H) (2)
を示せばよい。
(2) の仮定よりはじめて g'∈G',h'∈H とするとfは全射なので
g'=f(g) (g∈H ),h'=f(h) (h∈H)と書ける。
準同型写像の性質より
g'-1・h'・g'=f(g)-1・f(h)・f(g)=f(g-1)・f(h)・f(g)
=f(g-1hg)
仮定(1)よりg-1hg∈Hなので g'-1・h'・g'∈f(H) // 戻る
練習.2 と 練習.4 をセットにして考えたらよい。
練習5:a∈aN , b∈bN ⇒ ab∈abN=aNbN
( すなわちGの演算 ab にG/Nの演算 aNbN が対応している。)
// 戻る
304-1 [ 群Gの任意の要素aに対して aH=Ha をみたす部分群Hを正規部分群 ]
というのだから
G がアーベル群ならば(乗法において可換だから)その部分群 H はGの
任意の要素 a に対して aH=Ha をみたす。
ゆえにアーベル群の部分群はすべて正規部分群である。 //戻る
304-2 G の部分群 H の指数が 2 ならば G の任意の要素 a に対して
G = aN∪N かつ aN∩N = Φ
が成り立つ。
N は単位元だから Na≠N ゆえに Na=aN
したがって指数2の部分群 N は正規部分群である。 // 戻る
304-3 K= H1 ∩ H2 とおくとき G の任意の要素 g に対して gK = Kg を示せば
よい。
先ず gK⊂Kg を示す。
x∈gK とすると x=gk ( k∈K ) と書ける。
k∈H1 かつ k∈H2 なので gk∈gH1 かつ gk∈gH2
H1<G かつ H2<G なので gH1=H1g かつ gH2=H2g
∴ gk∈H1g かつ gk∈H2g
∴ gkg-1∈H1 かつ gkg-1∈H2
∴ gkg-1∈H1∩H2=K
∴ x=gk∈Kg ∴gK⊂Kg // 戻る
次に gK⊃Kg を示す。
y∈Kg とすると y=hg ( h∈K ) と書ける。
h∈H1 かつ h∈H2 なので hg∈H1g かつ hg∈H2g
H1<G かつ H2<G なので gH1=H1g かつ gH2=H2g
∴ hg∈gH1 かつ hg∈gH2
∴ g-1hg∈H1 かつ g-1hg∈H2
∴ g-1hg∈H1∩H2=K
∴ y=hg∈gK ∴gK⊃Kg // 戻る
304-4 H1⊂G , H2⊂G , H1 ∩ H2=K とおく、
h∈H1,x∈K に対して、H1⊂G だから hxh-1∈H1・・・(i)
またK⊂H2<G だから hxh-1∈H2 ・・・(ii)
(i),(ii) より hxh-1∈H1∩H2=K ∴ K = H1∩H2<H1 //戻る
しかしこの証明はちょっと自信ない。誤りが分かれば修正する。
304-5 これは H<G の定義そのものである。
HがGの正規部分群ならば、∀g∈Gに対して gH=Hg が成り立つ。
∀g∈G,∀h∈H に対して x = g-1hg とおくと gx = hg∈Hg
Hg = gH なので gx∈gH ∴ x∈H ∴ g-1hg∈H //戻る
代数の学習はともすれば上滑りになり勝ちである。
だから兎に角エンピツを持って書いて確かめることをしよう。
304-6 (0) a,b∈G ならば ab∈G ∴Ha・Hb = Hab∈{ H , Ha , Hb , ・・・ }
即ちこの演算について閉じている。
(1) Ha・(Hb・Hc) = Ha・Hbc = Ha・(b・c) = H(ab)c = Hab・Hc =(Ha・Hb)・Hc
即ち結合法則は成り立つ。
(2) Ha・H = Ha・He = Hae = Ha , H・Ha = He・Ha = Hea = Ha
即ち単位元は H である。
(3) Ha・Ha-1 = Ha・a-1 = He = H , Ha-1・Ha = Ha-1・a = He = H
即ち逆元は Ha-1 である。
以上により { H,Ha,Hb,・・・ } は群(剰余群)をなす。// 戻る
304-7 G/N がアーベル群ならば任意の a,b∈ N に対して
aNbN=bNaN ∴abN=baN ∴ab = ba
ところで
(ba)-1=a-1b-1 だから a-1b-1ab=(ba)-1ab=(ba)-1ba=e∈N // 戻る
304-8 (1) cos(θ1+θ2)+isin(θ1+θ2)=(cosθ1+isinθ1)・(cosθ2+isinθ2)
また、cosθ+isinθ=1 をみたすθは cosθ=1 , sinθ=0 より、
θ=2nπ n∈N //
(2) x1・x2→|x1・x2|=|x1|・|x2|
x1・x2→(x1・x2)2=(x1)2・(x2)2
x1・x2→1/(x1・x2)=(1/x1)・(1/x2)
いずれも 積に関して準同型対応:f(x1・x2)=f(x1)・f(x2)
である。 // 戻る
305-1 (1) Imf の任意の2元 x'=f(x) , y'=f(y) に対して
x'y'=f(x)f(y)=f(xy) , (x')-1=f(x)-1=f(x-1)
∴x'y'∈Imf,(x')-1∈Imf ゆえに、Imf はG'の部分群である。//戻る
(2) Kerf の任意の2元 x , y に対して、
先ず、f(x)=e' , f(y)=e' であるから、
f(xy)=f(x)f(y)=e'e'=e' , f(x-1)=f(x)-1=(e')-1=e'
∴ xy∈Kerf ,x-1∈Kerf ゆえに、KerfはGの部分群である。
つぎに、Gの任意の元 a とKerf の元k にたいして、
f(a-1ka)=f(a-1)f(k)f(a)=f(a)-1e'f(a)=f(a)-1f(a)=e'
∴ a-1ka∈Kerf ∴ Kerf<G //戻る
305-2 (1) Imf の定義から明らかである。
//戻る
(2) f(e)=e' であるが、f が単射ならば、e 以外に e' に
移る元は存在しない。 ∴ Kerf={e}
逆に、Kerf={e} とするとき、
f(x)=f(y) ならば、両辺に f(y)-1 を右乗して、
f(x)f(y)-1=f(y)f(y)-1 ∴ f(xy-1)=e'
∴ xy-1=e ∴ x=y したがって f は単射である。 //戻る
305-3 写像 p が全射になることは明らかである。
さらに、Gの任意の元 x , y にたいして p(xy)=Kxy=KxKy=p(x)p(y)
が成り立つから、p は準同型写像である。 // 戻る
しかし、この事実はほとんど明らかなことである。
305-4 K=Kerf とおき、G/K から Imfへの写像 ψ を Kx →x'=f(x) に
よって定義するとき、ψ が同型写像になることを示せばよい。
まず、Kx=Ky とすれば、x=ky ( k ∈K ) とおけるから定義により、
ψ(Kx)=f(x) =f(ky)=f(k)f(y) = e'f(y) = f(y) = ψ(Ky)
であるから、ψ は確かに(一意的)写像である。
逆に、ψ(Kx) = ψ(Ky) とすれば、f(x) = f(y) であるから、
Kx = Ky したがって、ψ は単射である。
さらに、Imf の任意の元を x' とすれば、x'=f(x) ( x ∈G )
とおけるから定義により、
x' = f(x)=ψ(Kx) したがって、ψ は全射である。
最後に、 G の任意の2元 x , y にたいして、
ψ(KxKy) = ψ(Kxy) = f(xy) = f(x)f(y) =ψ(Kx)ψ(Ky)
であるから、ψ は準同型写像である。
以上によって, ψ は同型写像である。 // 戻る
305-5 それぞれ、つぎの準同型写像 f に準同型定理を適用すればよい。
(1) f(x)=e ( x ∈G ) (2) f(x)=x ( x ∈G )
「準同型定理を適用」とは如何なることか? // 戻る
305-6 K<G ならば、f をG からG/K の上への自然
な準同型写像とするとき、Kerf=K となる。
逆は問題305-1(2)から明らかである。 // 戻る
305-7 RからTの上への準同型写像 f : x → ei2πx に準同型定理を
適用すればよい。
「準同型定理を適用」とは如何なることか? // 戻る
305-8 (1) f の定義域をHに制限すれば、fはHからG'への準同型写像で
あるから、その像H'はG'の部分群である。
つぎに、fはGからG'の上への写像であるから、G'の任意の元 a'
にたいして a'=f(a) ( a∈G ) とおける。したがって、
(a')-1H'a'=f(a)-1f(H)f(a)=f(a-1Ha)=f(H)=H' ∴ H'
A4の部分群:K={(1),(12)(34),(13)(24),(14)(23)} について、
e=(1),p=(12)(34),q=(13)(24),r=(14)(23)
とおいたときのKの乗積表を左に示す。
左対角線を軸に対称となり、アーベル群である。
また、Kの中に位数2の部分群:{e,p},{e,q},{e,r}
があることも分る。
戻る
練習1:(12)→(12)(12)(12)=(12) は明らか。
(13)→(12)(13)(12)=(123)(12)=(213)=(132)=(23)
(23)→(12)(23)(12)=(12)((12)(13)(12))(12) (上の結果を用いた)
=((12)(12))(13)((12)(12))=(13)
(123)→(12)(123)(12)=(12)((12)(13))(12)
=((12)(12))(13)(12)=(13)(12)=(132)
(132)→(12)(132)(12)=(12)((13)(12))(12)
=((12)(13))(12)(12)=(12)(13)=(123) //
すなわち、S3の内部自己同型は全単射であるから同型対応であり、
S3と一致する。
したがって、後で述べることになるがS3は正規部分群である。
戻る
練習2:f:G → G'(準同型対応) のもとで H:Gの部分群→f(H):G'の部分群
を示したい。
それは即ち
仮定:h1 , h2∈H ⇒ h1・h2-1∈H (1)
結論:h'1 , h'2∈f(H) ⇒ h'1・h'2-1∈f(H) (2)
を示すことである。
(2) の仮定より始めて h'1 , h'2∈f(H) とすると
h'1=f(h1) , h2'=f(h2) ( h1 , h2∈H )
と書ける。
準同型写像の性質から
h'1・h'2-1=f(h1)・f(h2)-1=f(h1)・f(h2-1)=f(h1・h2-1)∈f(H)
これで (2) が示せた。 //戻る
練習3:S3={1,(12),(13),(23),(123),(132)} について、
交代群A3={1,(123),(132)}の (23)による内部同型置換 を求めると、
(23)1(23)=1
(23)(123)(23)=(23)(231)(23)=(23)(23)(21)(23)
=(21)(23)=(213)=(132)
(23)(132)(23)=(23)(213)(23)=(23)(21)(23)(23)
=(23)(21)=(231)=(123)
同様に
S3 の任意の元a による1,(123),(132)の内部同型置換は 1,(123),(132)に
1対1で対応する。すなわち、
S3の任意の元aについてa-1A3a=A3が成り立つからA3は正規部分群である。//
また、S4 の元例えば(12)による交代群A4の内部同型置換をすると、
(12)A4(12)=A4が成り立つ。何故ならば、
A4は偶置換の集合だからS4の任意の元、例えば(12)
に対してA4(12)、(12)A4は共に奇置換の集合であり、
A4(12)∪A4=(12)A4∪A4=S4 , A4(12)∩A4=(12)A4∩A4=φ
∴A4(12)=(12)A4 ∴(12)A4(12)=(12)(12)A4=A4
すなわち、
S4の元aについて a-1A4a=A4 だから A4 は正規部分群である。 // 戻る
練習4:f が全射という意味は: ∀g'∈G',∃g∈G ; f(g)=g'であることをいう。
( G'の任意(arbitrary)の元g'に対して f(g)=g'をみたすGの元g
が存在する(exist) ということ。)
練習2.でf(H)がG'の部分群であることは示されているから、あとは
f(H)が正規部分群の条件をみたしていることを示せばよい。
すなわち
仮定:g∈G,h∈H ⇒ g-1hg∈H (1)
結論:g'∈G',h'∈H ⇒ g'-1・h'・g'∈f(H) (2)
を示せばよい。
(2) の仮定よりはじめて g'∈G',h'∈H とするとfは全射なので
g'=f(g) (g∈H ),h'=f(h) (h∈H)と書ける。
準同型写像の性質より
g'-1・h'・g'=f(g)-1・f(h)・f(g)=f(g-1)・f(h)・f(g)
=f(g-1hg)
仮定(1)よりg-1hg∈Hなので g'-1・h'・g'∈f(H) // 戻る
練習.2 と 練習.4 をセットにして考えたらよい。
練習5:a∈aN , b∈bN ⇒ ab∈abN=aNbN
( すなわちGの演算 ab にG/Nの演算 aNbN が対応している。)
// 戻る
304-1 [ 群Gの任意の要素aに対して aH=Ha をみたす部分群Hを正規部分群 ]
というのだから
G がアーベル群ならば(乗法において可換だから)その部分群 H はGの
任意の要素 a に対して aH=Ha をみたす。
ゆえにアーベル群の部分群はすべて正規部分群である。 //戻る
304-2 G の部分群 H の指数が 2 ならば G の任意の要素 a に対して
G = aN∪N かつ aN∩N = Φ
が成り立つ。
N は単位元だから Na≠N ゆえに Na=aN
したがって指数2の部分群 N は正規部分群である。 // 戻る
304-3 K= H1 ∩ H2 とおくとき G の任意の要素 g に対して gK = Kg を示せば
よい。
先ず gK⊂Kg を示す。
x∈gK とすると x=gk ( k∈K ) と書ける。
k∈H1 かつ k∈H2 なので gk∈gH1 かつ gk∈gH2
H1<G かつ H2<G なので gH1=H1g かつ gH2=H2g
∴ gk∈H1g かつ gk∈H2g
∴ gkg-1∈H1 かつ gkg-1∈H2
∴ gkg-1∈H1∩H2=K
∴ x=gk∈Kg ∴gK⊂Kg // 戻る
次に gK⊃Kg を示す。
y∈Kg とすると y=hg ( h∈K ) と書ける。
h∈H1 かつ h∈H2 なので hg∈H1g かつ hg∈H2g
H1<G かつ H2<G なので gH1=H1g かつ gH2=H2g
∴ hg∈gH1 かつ hg∈gH2
∴ g-1hg∈H1 かつ g-1hg∈H2
∴ g-1hg∈H1∩H2=K
∴ y=hg∈gK ∴gK⊃Kg // 戻る
304-4 H1⊂G , H2⊂G , H1 ∩ H2=K とおく、
h∈H1,x∈K に対して、H1⊂G だから hxh-1∈H1・・・(i)
またK⊂H2<G だから hxh-1∈H2 ・・・(ii)
(i),(ii) より hxh-1∈H1∩H2=K ∴ K = H1∩H2<H1 //戻る
しかしこの証明はちょっと自信ない。誤りが分かれば修正する。
304-5 これは H<G の定義そのものである。
HがGの正規部分群ならば、∀g∈Gに対して gH=Hg が成り立つ。
∀g∈G,∀h∈H に対して x = g-1hg とおくと gx = hg∈Hg
Hg = gH なので gx∈gH ∴ x∈H ∴ g-1hg∈H //戻る
代数の学習はともすれば上滑りになり勝ちである。
だから兎に角エンピツを持って書いて確かめることをしよう。
304-6 (0) a,b∈G ならば ab∈G ∴Ha・Hb = Hab∈{ H , Ha , Hb , ・・・ }
即ちこの演算について閉じている。
(1) Ha・(Hb・Hc) = Ha・Hbc = Ha・(b・c) = H(ab)c = Hab・Hc =(Ha・Hb)・Hc
即ち結合法則は成り立つ。
(2) Ha・H = Ha・He = Hae = Ha , H・Ha = He・Ha = Hea = Ha
即ち単位元は H である。
(3) Ha・Ha-1 = Ha・a-1 = He = H , Ha-1・Ha = Ha-1・a = He = H
即ち逆元は Ha-1 である。
以上により { H,Ha,Hb,・・・ } は群(剰余群)をなす。// 戻る
304-7 G/N がアーベル群ならば任意の a,b∈ N に対して
aNbN=bNaN ∴abN=baN ∴ab = ba
ところで
(ba)-1=a-1b-1 だから a-1b-1ab=(ba)-1ab=(ba)-1ba=e∈N // 戻る
304-8 (1) cos(θ1+θ2)+isin(θ1+θ2)=(cosθ1+isinθ1)・(cosθ2+isinθ2)
また、cosθ+isinθ=1 をみたすθは cosθ=1 , sinθ=0 より、
θ=2nπ n∈N //
(2) x1・x2→|x1・x2|=|x1|・|x2|
x1・x2→(x1・x2)2=(x1)2・(x2)2
x1・x2→1/(x1・x2)=(1/x1)・(1/x2)
いずれも 積に関して準同型対応:f(x1・x2)=f(x1)・f(x2)
である。 // 戻る
305-1 (1) Imf の任意の2元 x'=f(x) , y'=f(y) に対して
x'y'=f(x)f(y)=f(xy) , (x')-1=f(x)-1=f(x-1)
∴x'y'∈Imf,(x')-1∈Imf ゆえに、Imf はG'の部分群である。//戻る
(2) Kerf の任意の2元 x , y に対して、
先ず、f(x)=e' , f(y)=e' であるから、
f(xy)=f(x)f(y)=e'e'=e' , f(x-1)=f(x)-1=(e')-1=e'
∴ xy∈Kerf ,x-1∈Kerf ゆえに、KerfはGの部分群である。
つぎに、Gの任意の元 a とKerf の元k にたいして、
f(a-1ka)=f(a-1)f(k)f(a)=f(a)-1e'f(a)=f(a)-1f(a)=e'
∴ a-1ka∈Kerf ∴ Kerf<G //戻る
305-2 (1) Imf の定義から明らかである。
//戻る
(2) f(e)=e' であるが、f が単射ならば、e 以外に e' に
移る元は存在しない。 ∴ Kerf={e}
逆に、Kerf={e} とするとき、
f(x)=f(y) ならば、両辺に f(y)-1 を右乗して、
f(x)f(y)-1=f(y)f(y)-1 ∴ f(xy-1)=e'
∴ xy-1=e ∴ x=y したがって f は単射である。 //戻る
305-3 写像 p が全射になることは明らかである。
さらに、Gの任意の元 x , y にたいして p(xy)=Kxy=KxKy=p(x)p(y)
が成り立つから、p は準同型写像である。 // 戻る
しかし、この事実はほとんど明らかなことである。
305-4 K=Kerf とおき、G/K から Imfへの写像 ψ を Kx →x'=f(x) に
よって定義するとき、ψ が同型写像になることを示せばよい。
まず、Kx=Ky とすれば、x=ky ( k ∈K ) とおけるから定義により、
ψ(Kx)=f(x) =f(ky)=f(k)f(y) = e'f(y) = f(y) = ψ(Ky)
であるから、ψ は確かに(一意的)写像である。
逆に、ψ(Kx) = ψ(Ky) とすれば、f(x) = f(y) であるから、
Kx = Ky したがって、ψ は単射である。
さらに、Imf の任意の元を x' とすれば、x'=f(x) ( x ∈G )
とおけるから定義により、
x' = f(x)=ψ(Kx) したがって、ψ は全射である。
最後に、 G の任意の2元 x , y にたいして、
ψ(KxKy) = ψ(Kxy) = f(xy) = f(x)f(y) =ψ(Kx)ψ(Ky)
であるから、ψ は準同型写像である。
以上によって, ψ は同型写像である。 // 戻る
305-5 それぞれ、つぎの準同型写像 f に準同型定理を適用すればよい。
(1) f(x)=e ( x ∈G ) (2) f(x)=x ( x ∈G )
「準同型定理を適用」とは如何なることか? // 戻る
305-6 K<G ならば、f をG からG/K の上への自然
な準同型写像とするとき、Kerf=K となる。
逆は問題305-1(2)から明らかである。 // 戻る
305-7 RからTの上への準同型写像 f : x → ei2πx に準同型定理を
適用すればよい。
「準同型定理を適用」とは如何なることか? // 戻る
305-8 (1) f の定義域をHに制限すれば、fはHからG'への準同型写像で
あるから、その像H'はG'の部分群である。
つぎに、fはGからG'の上への写像であるから、G'の任意の元 a'
にたいして a'=f(a) ( a∈G ) とおける。したがって、
(a')-1H'a'=f(a)-1f(H)f(a)=f(a-1Ha)=f(H)=H' ∴ H' G'
// 戻る
(2) G'からG'/H'の上への自然な準同型写像を p' とし、φ= p'・f
とおけば、φ は G から G'/H' の上への準同型写像になる。
したがって、その核 H=Kerφ はG の正規部分群になる。
(3) (2) の φ に準同型定理を適用すればよい。// 戻る
305-9 H ⊂G , K<G , HK ⊂G だから問304-4 により、H∩K<H
かつ、問305-4 により
H/(H∩K) G'
// 戻る
(2) G'からG'/H'の上への自然な準同型写像を p' とし、φ= p'・f
とおけば、φ は G から G'/H' の上への準同型写像になる。
したがって、その核 H=Kerφ はG の正規部分群になる。
(3) (2) の φ に準同型定理を適用すればよい。// 戻る
305-9 H ⊂G , K<G , HK ⊂G だから問304-4 により、H∩K<H
かつ、問305-4 により
H/(H∩K)  HK/Kを得る。 // 戻る
305-10 G からG/H への自然な準同型写像を p とすれば、第1同型定理
により、p によって G の正規部分群 K はG/H の正規部分群 K/H に
移され , (G/H)(K/H) HK/Kを得る。 // 戻る
305-10 G からG/H への自然な準同型写像を p とすれば、第1同型定理
により、p によって G の正規部分群 K はG/H の正規部分群 K/H に
移され , (G/H)(K/H) G/K // 戻る
306-1 S2={(1) ,(23)}の乗積表は e=(1) , p=(23)とおくと、 G/K // 戻る
306-1 S2={(1) ,(23)}の乗積表は e=(1) , p=(23)とおくと、 右のとおりであり、S2の位数は2。部分群は{e}。
したがって、S2>{e} であり、S2はアーベル群だから可解群である。 //
S3については e=(1), a=(132), b=(123), p=(23), q=(13), r=(12) とおくと、
右のとおりであり、S2の位数は2。部分群は{e}。
したがって、S2>{e} であり、S2はアーベル群だから可解群である。 //
S3については e=(1), a=(132), b=(123), p=(23), q=(13), r=(12) とおくと、
 その乗積表は右のとおりである。
S3の部分群は問303-1で見たとおり
{e,p} , {e,q} , {e,r} , {e,a,b} の4個ある。
このうち、{e,a,b}={(1),(132),(123)}=A3である。
S3の位数は6であり、A3の位数は3だから、A3のS3における指数=6/3=2(素数)。
A3はS3の最大の正規部分群である。
A3の位数=3 の約数は 3と1 だから部分群はA3と{e}。
したがって、S3>A3
その乗積表は右のとおりである。
S3の部分群は問303-1で見たとおり
{e,p} , {e,q} , {e,r} , {e,a,b} の4個ある。
このうち、{e,a,b}={(1),(132),(123)}=A3である。
S3の位数は6であり、A3の位数は3だから、A3のS3における指数=6/3=2(素数)。
A3はS3の最大の正規部分群である。
A3の位数=3 の約数は 3と1 だから部分群はA3と{e}。
したがって、S3>A3 {e} であり、
剰余群列S3/A3 , A3/{e} の各位数は 2,3(いずれも素数)。
よって、S3は可解群である。 // 戻る
( つぎの問306-2のS4が可解群であることが分っていれば、S2,S3は
共にS4の部分群であるから、定理6によりいずれも可解群になる。)
306-2 S4は1234の順列の集合だから元の個数は4!=1・2・3・4=24個。
S4の半分は偶置換の集合すなわち交代群A4である。問303-3で求めたとおり、
A4={ (1), (123), (132), (124), (142), (134), (143),
(234), (243), (12)(34), (13)(24), (14)(23) }
A4の各元に例えば(12)を掛けた集合 (12)A4は奇置換の集合になる。
ゆえにA4はS4の最大の正規部分群である。
A4の部分群として K={ (1), (12)(34), (13)(24), (14)(23) } を作る。
K の各元は共通の数字をもたない互換の積だからKは正規部分群であり、
( 注: Kの(1)以外の3個の元に1つの置換を施すということは畢竟1234を
或る一定の順序に入れ換えることに他ならないのだから、これら
3個の元以外にはならない。故にaK=Ka,(∀a∈A4) )
KのA4における指数が12/4=3(素数)だからKはA4の最大の正規部分群である。
Kの部分群として L={ (1), (12)(34) } をつくると LはKの正規部分群で
あり、LのKにおける指数は2(素数)だから、LはKの最大の正規部分群である。
よって、S4の正規列:S4>A4>K>L>e ができる。また、
剰余群列:S4/A4,A4/K,K/L,L/e(=L)の各位数は 2,3,2,2(素数)であるから、
S4は可解群である。 // 戻る
306-3 生成元をσとして部分群をすべて求めてみれば、G(全体の群)、E(単位群)
の他にσ2,σ3,σ4,σ6を生成元とする巡回群H2,H3,H4,H6が存在し、
下図のような関係にある。 {e} であり、
剰余群列S3/A3 , A3/{e} の各位数は 2,3(いずれも素数)。
よって、S3は可解群である。 // 戻る
( つぎの問306-2のS4が可解群であることが分っていれば、S2,S3は
共にS4の部分群であるから、定理6によりいずれも可解群になる。)
306-2 S4は1234の順列の集合だから元の個数は4!=1・2・3・4=24個。
S4の半分は偶置換の集合すなわち交代群A4である。問303-3で求めたとおり、
A4={ (1), (123), (132), (124), (142), (134), (143),
(234), (243), (12)(34), (13)(24), (14)(23) }
A4の各元に例えば(12)を掛けた集合 (12)A4は奇置換の集合になる。
ゆえにA4はS4の最大の正規部分群である。
A4の部分群として K={ (1), (12)(34), (13)(24), (14)(23) } を作る。
K の各元は共通の数字をもたない互換の積だからKは正規部分群であり、
( 注: Kの(1)以外の3個の元に1つの置換を施すということは畢竟1234を
或る一定の順序に入れ換えることに他ならないのだから、これら
3個の元以外にはならない。故にaK=Ka,(∀a∈A4) )
KのA4における指数が12/4=3(素数)だからKはA4の最大の正規部分群である。
Kの部分群として L={ (1), (12)(34) } をつくると LはKの正規部分群で
あり、LのKにおける指数は2(素数)だから、LはKの最大の正規部分群である。
よって、S4の正規列:S4>A4>K>L>e ができる。また、
剰余群列:S4/A4,A4/K,K/L,L/e(=L)の各位数は 2,3,2,2(素数)であるから、
S4は可解群である。 // 戻る
306-3 生成元をσとして部分群をすべて求めてみれば、G(全体の群)、E(単位群)
の他にσ2,σ3,σ4,σ6を生成元とする巡回群H2,H3,H4,H6が存在し、
下図のような関係にある。
群の間の数字は指数を示す。たとえば(H2:H6)=3.
図上でGからEに至る道をもとめて次の3通りの
正規列が得られる。
G>H3>H6>E
G>H2>H6>E
G>H2>H4>E
|  |
戻る
306-4
この論証には自信がない。メモである。後日分り次第訂正する。
H1={1,i,j,k} , H2={-1,-i,-j,-k} とおくと、G={H1,H2}
(-1)H1=H2 , (-1)H2=H1 , (-1)H1(-1)=H1 , (-1)H2(-1)=H2
∴G>H1
かつ、 H1H1=H2H2 , H1H2=H2H1 ゆえにGは可解群である。// 戻る
306-5
∀aba-1b-1∈G'のとき
G/N がAbel群ならば、ab=ba だから、aba-1b-1=ab(ba)-1=ba(ba)-1=e∈N
∴N ⊃ G 戻る
306-6 暫定解:あとで訂正する。
S3について、e=(1), a=(132), b=(123), p=(23), q=(13), r=(12) とおいて、
 対応する2つの元の交換子 x-1y-1xy を
求めて一覧表をつくると、右のようになる。
それ故、S3の交換子群は { e , a , b } すなわちA3に等しい。
表から、交代群A3={ e , a , b }の交換子群は{e}であることが分る。//
一般にアーベル群の交換子群は{e}である。← x-1y-1xy=(yx)-1xy=(yx)-1yx=e
しかし交換子群は{e}であってもその群がアーベル群であるとは
いえないことも上の表から分る。← {p,q,r} 戻る
306-7
abcxy の順列が置換(ab)によってbacxyになることを [abcxy](ab)=[bacxy]
と表すことにすると、
[abcxy](xab)(byc)(xab)-1(byc)-1=[bxcay](byc)(xab)-1(byc)-1
=[yxbac](xab)-1(byc)-1
=[ybaxc](byc)-1
=[bcaxy]
また、[abcxy](abc)=[bcaxy]
∴(xab)(byc)(xab)-1(byc)-1=(abc) // 戻る
401-1 ユークリッドの互除法による。
g を φ で割った商を q1 余りを r1
φ を r1 で割った商を q2 余りを r2
r1 を r2 で割った商を q3 余りを 0
とすると、
g=φ・q1+r1 , φ=r1・q2+r2 , r1=r2・q3
a,b の最大公約数を (a,b) と書くことにすると以上のことから、
r2=(r2,r1)=(r1,φ)=(φ,g)
このとき、r2 は g と φ の最大公約数 d である。
∴ d=r2=φ-r1・q2=φ-(g-φ・q1)・q2 = (1+q1・q2)・φ+(q2)・g
戻る
401-2(1) c0+c1α ci∈k
(2) c0+c1α+c2α2 ci∈k
(3) c0+c1α+c2αβ+c3β ci∈k
(4)
対応する2つの元の交換子 x-1y-1xy を
求めて一覧表をつくると、右のようになる。
それ故、S3の交換子群は { e , a , b } すなわちA3に等しい。
表から、交代群A3={ e , a , b }の交換子群は{e}であることが分る。//
一般にアーベル群の交換子群は{e}である。← x-1y-1xy=(yx)-1xy=(yx)-1yx=e
しかし交換子群は{e}であってもその群がアーベル群であるとは
いえないことも上の表から分る。← {p,q,r} 戻る
306-7
abcxy の順列が置換(ab)によってbacxyになることを [abcxy](ab)=[bacxy]
と表すことにすると、
[abcxy](xab)(byc)(xab)-1(byc)-1=[bxcay](byc)(xab)-1(byc)-1
=[yxbac](xab)-1(byc)-1
=[ybaxc](byc)-1
=[bcaxy]
また、[abcxy](abc)=[bcaxy]
∴(xab)(byc)(xab)-1(byc)-1=(abc) // 戻る
401-1 ユークリッドの互除法による。
g を φ で割った商を q1 余りを r1
φ を r1 で割った商を q2 余りを r2
r1 を r2 で割った商を q3 余りを 0
とすると、
g=φ・q1+r1 , φ=r1・q2+r2 , r1=r2・q3
a,b の最大公約数を (a,b) と書くことにすると以上のことから、
r2=(r2,r1)=(r1,φ)=(φ,g)
このとき、r2 は g と φ の最大公約数 d である。
∴ d=r2=φ-r1・q2=φ-(g-φ・q1)・q2 = (1+q1・q2)・φ+(q2)・g
戻る
401-2(1) c0+c1α ci∈k
(2) c0+c1α+c2α2 ci∈k
(3) c0+c1α+c2αβ+c3β ci∈k
(4)  cijαiβj ( cij∈k , 0≤i≤2 , 0≤j≤2)
(5) cijαiβj ( cij∈k , 0≤i≤2 , 0≤j≤2)
(5)  cijαiβj ( cij∈k , 0≤i≤3 , 0≤j≤3)
戻る
401-3(1) x4-2x2+9=0 x4-2x2+1=-8 (x2-1)2=-8
x2=1±2 cijαiβj ( cij∈k , 0≤i≤3 , 0≤j≤3)
戻る
401-3(1) x4-2x2+9=0 x4-2x2+1=-8 (x2-1)2=-8
x2=1±2 i = ( i = ( +i)2
∴x= +i)2
∴x=  +i , +i ,  -i , - -i , - +i , - +i , - -i //
(2) θ= -i //
(2) θ= +i とすれば、θ2=1+2 +i とすれば、θ2=1+2 i
∴θ3=θ2・θ=(1+2 i
∴θ3=θ2・θ=(1+2 i)( i)( +i)= +i)= -2 -2 +(4+1)i=- +(4+1)i=- +5i
上の2式より i と +5i
上の2式より i と をそれぞれ消去して
5θ-θ3=6 をそれぞれ消去して
5θ-θ3=6 , θ+θ3=6i
∴ , θ+θ3=6i
∴  =(5θ-θ3)/6 , i=(θ+θ3)/6 // 戻る
401-4
α3-6α2+4α+2=0 ∴α3=6α2-4α-2 両辺にαを掛けて、
∴α4=6α3-4α2-2α
=6(6α2-4α-2)-4α2-2α ( ← α3=6α2-4α-2 )
=32α2-26α-12 //
α6=α4・α2=(32α2-26α-12)・α2
=32α4-26α3-12α2
=32(32α2-26α-12)-26(6α2-4α-2)-12α2
=(32・32-26・6-12)α2-(32・26-26・4)α-(32・12-26・2)
=856α2-728α-332 //
α3-6α2+4α+2=0 ∴1=α3-6α2+4α+3=(α+1)(α2-7α+11)-8
∴(α+1)(α2-7α+11)=9
∴1/(α+1)=(α2-7α+11)/9
∴α+1/(α+1)=α+(α2-7α+11)/9=(α2+2α+11)/9 //
戻る
401-5
x=1+ =(5θ-θ3)/6 , i=(θ+θ3)/6 // 戻る
401-4
α3-6α2+4α+2=0 ∴α3=6α2-4α-2 両辺にαを掛けて、
∴α4=6α3-4α2-2α
=6(6α2-4α-2)-4α2-2α ( ← α3=6α2-4α-2 )
=32α2-26α-12 //
α6=α4・α2=(32α2-26α-12)・α2
=32α4-26α3-12α2
=32(32α2-26α-12)-26(6α2-4α-2)-12α2
=(32・32-26・6-12)α2-(32・26-26・4)α-(32・12-26・2)
=856α2-728α-332 //
α3-6α2+4α+2=0 ∴1=α3-6α2+4α+3=(α+1)(α2-7α+11)-8
∴(α+1)(α2-7α+11)=9
∴1/(α+1)=(α2-7α+11)/9
∴α+1/(α+1)=α+(α2-7α+11)/9=(α2+2α+11)/9 //
戻る
401-5
x=1+ とおくと、x-1= とおくと、x-1= ∴ (x-1)2=2 ∴ x2-2x-1=0 //
x=2+ ∴ (x-1)2=2 ∴ x2-2x-1=0 //
x=2+ とおくと、x-2= とおくと、x-2= ∴ (x-2)3=2 ∴ x3-6x2+12x-8=2
∴ x3-6x2+12x-10=0 //
x= ∴ (x-2)3=2 ∴ x3-6x2+12x-8=2
∴ x3-6x2+12x-10=0 //
x= + + とおくと、x2=5+2 とおくと、x2=5+2  ∴(x2-5)2=24 ∴x4-10x2+1=0 //
戻る
401-6
2つの体K1,K2の元の間に1対1の対応があって、
a1←→a2 , b1←→b2 のとき、a1+b1←→a2+b2 , a1・b1←→a2・b2
であれば、K1,K2は同型であるといい、その対応を同型対応という.
とくに、体Kのそれ自身への上への同型対応を自己同型対応という.
例えば、
複素数体において、対応:a+bi←→a-bi は自己同型対応である.
戻る
401-7
α,βがk(x)の既約な多項式φ(x)の根であるとき、2つの体
k(α)とk(β)について、
同型の意味については前問でほぼ説明している.
同値であるとはk の元をそれ自身に対応させる対応(つまりkの元を
動かさない対応)でk(α)とk(β)が同型であることをいう.
(だから、同値は同型よりも強い条件である.)
またそのような対応のことをk-同型対応 という.
α,βがk(x)の既約な多項式φ(x)の根であるとき、k(α),k(β)
を kに関して互いに共役であるという.
また、
k(α),k(β)の元f(α),f(β)をkに関して互いに共役な元という.
戻る
402-1
αをf(x)=0 のk重根とすると、
f(x)=(x-α)kg(x) xで微分して・・・
∴f'(x)=k(x-α)k-1g(x)+(x-α)kg'(x)
=(x-α)k-1(kg(x)+(x-α)g'(x)) // 戻る
402-2
φ(x)がk重根をもてば402-1の考察によってφ'(x)はk-1重根をもつから
φ(x)とφ'(x)にG.C.M d(x)が存在するとすればそれはφ(x)より低次である.
戻る
402-3
γ=cα + β と βj = γ - cαi から cα + β = βj + cαi
∴ c・(α - αi) = βj - β ∴ c(αi-α)+(βj-β)=0 //
戻る
402-4 定理6.の論議の要点は・・・
α,βが満足するk[x]の既約多項式をそれぞれf(x),g(x)とし、
cαi+βj≠cαi'+βj' のような c を1つとって
γ = cα+β とおけば k(α,β) = k(γ) ・・・ということであるから、
その一般化としての定理7を先ずつぎのように書き直す.
定理7'.(n=2 のときが定理6である.)
α1,α2,・・・・・・,αnが k[x]の既約多項式:f1(x),f2(x),・・・・・・,fn(x)
の根ならば、
k(α1,α2,・・・・・・,αn)は kの単純拡大である.
ただし、αi= αi1,αi2,・・・・・・,αim , i=1,2,3,・・・,n
証明を考える・・・形式的には以下のようになるだろうか.
n=1 のとき、k にf1(x)の根α1を添加して、k(α1)を得る.
n=2 のとき、k(α1)に f2(x)の根α2 を添加する.
cα1i+α2j≠cα1i'+α2j' のような c を1つとって
γ2=cα1+α2 とおけば k(α1,α2)=k(γ2)( 定理6の証明)
n=k のとき、k(γk-1)に fk(x)の根αk を添加する.
cγ(k-1)i+αkj≠cγ(k-1)i'+αkj'のような c を1つとって
γk = cγk-1+αk とおけば
k(γk-1,αk)=k(α1,α2,・・・・・・,αk-1,αk)=k(γk)
∴ k(α1,α2,・・・・・・,αn)=k(γn) //
γn は γn=c1α1+c2α2+・・・・・・+cnαn の形であるが、
c1 , c2 , ・・・・・・ , cn はつぎのように定る.
γ2=b1α1+α2
γ3=b2α2+α3=b2(b1α1+α2)+α3=b1b2α1+b2α2+α3
γ4=b3α3+α4=b3(b1b2α1+b2α2+α3)+α4
=b1b2b3α1+b2b3α2+b3α3+α4
∴ n=4 のとき、c1=b1b2b3 , c2=b2b3 , c3=b3 , c4=1 以下同様に、
n=5 のとき、c1=b1b2b3b4 , c2=b2b3b4 , c3=b3b4 , c4=b4 , c5=1
戻る ∴(x2-5)2=24 ∴x4-10x2+1=0 //
戻る
401-6
2つの体K1,K2の元の間に1対1の対応があって、
a1←→a2 , b1←→b2 のとき、a1+b1←→a2+b2 , a1・b1←→a2・b2
であれば、K1,K2は同型であるといい、その対応を同型対応という.
とくに、体Kのそれ自身への上への同型対応を自己同型対応という.
例えば、
複素数体において、対応:a+bi←→a-bi は自己同型対応である.
戻る
401-7
α,βがk(x)の既約な多項式φ(x)の根であるとき、2つの体
k(α)とk(β)について、
同型の意味については前問でほぼ説明している.
同値であるとはk の元をそれ自身に対応させる対応(つまりkの元を
動かさない対応)でk(α)とk(β)が同型であることをいう.
(だから、同値は同型よりも強い条件である.)
またそのような対応のことをk-同型対応 という.
α,βがk(x)の既約な多項式φ(x)の根であるとき、k(α),k(β)
を kに関して互いに共役であるという.
また、
k(α),k(β)の元f(α),f(β)をkに関して互いに共役な元という.
戻る
402-1
αをf(x)=0 のk重根とすると、
f(x)=(x-α)kg(x) xで微分して・・・
∴f'(x)=k(x-α)k-1g(x)+(x-α)kg'(x)
=(x-α)k-1(kg(x)+(x-α)g'(x)) // 戻る
402-2
φ(x)がk重根をもてば402-1の考察によってφ'(x)はk-1重根をもつから
φ(x)とφ'(x)にG.C.M d(x)が存在するとすればそれはφ(x)より低次である.
戻る
402-3
γ=cα + β と βj = γ - cαi から cα + β = βj + cαi
∴ c・(α - αi) = βj - β ∴ c(αi-α)+(βj-β)=0 //
戻る
402-4 定理6.の論議の要点は・・・
α,βが満足するk[x]の既約多項式をそれぞれf(x),g(x)とし、
cαi+βj≠cαi'+βj' のような c を1つとって
γ = cα+β とおけば k(α,β) = k(γ) ・・・ということであるから、
その一般化としての定理7を先ずつぎのように書き直す.
定理7'.(n=2 のときが定理6である.)
α1,α2,・・・・・・,αnが k[x]の既約多項式:f1(x),f2(x),・・・・・・,fn(x)
の根ならば、
k(α1,α2,・・・・・・,αn)は kの単純拡大である.
ただし、αi= αi1,αi2,・・・・・・,αim , i=1,2,3,・・・,n
証明を考える・・・形式的には以下のようになるだろうか.
n=1 のとき、k にf1(x)の根α1を添加して、k(α1)を得る.
n=2 のとき、k(α1)に f2(x)の根α2 を添加する.
cα1i+α2j≠cα1i'+α2j' のような c を1つとって
γ2=cα1+α2 とおけば k(α1,α2)=k(γ2)( 定理6の証明)
n=k のとき、k(γk-1)に fk(x)の根αk を添加する.
cγ(k-1)i+αkj≠cγ(k-1)i'+αkj'のような c を1つとって
γk = cγk-1+αk とおけば
k(γk-1,αk)=k(α1,α2,・・・・・・,αk-1,αk)=k(γk)
∴ k(α1,α2,・・・・・・,αn)=k(γn) //
γn は γn=c1α1+c2α2+・・・・・・+cnαn の形であるが、
c1 , c2 , ・・・・・・ , cn はつぎのように定る.
γ2=b1α1+α2
γ3=b2α2+α3=b2(b1α1+α2)+α3=b1b2α1+b2α2+α3
γ4=b3α3+α4=b3(b1b2α1+b2α2+α3)+α4
=b1b2b3α1+b2b3α2+b3α3+α4
∴ n=4 のとき、c1=b1b2b3 , c2=b2b3 , c3=b3 , c4=1 以下同様に、
n=5 のとき、c1=b1b2b3b4 , c2=b2b3b4 , c3=b3b4 , c4=b4 , c5=1
戻る
|
 ( a,bは有理数 ) について
(a+b
( a,bは有理数 ) について
(a+b

 正方形を移動して頂点1234がABCDになったことを(ABCD)
とかくことにすると、その移動はつぎの8個になる。
e=(1234) , a=(2341) , b=(3412) , c=(4123)
p=(24) , q=(13) , r=(14)(23) , s=(12)(34)
これらの移動について、乗積表(群表)をつくる。
例:ab=(2341)(3412)=(4123)=c 以下略。
正方形を移動して頂点1234がABCDになったことを(ABCD)
とかくことにすると、その移動はつぎの8個になる。
e=(1234) , a=(2341) , b=(3412) , c=(4123)
p=(24) , q=(13) , r=(14)(23) , s=(12)(34)
これらの移動について、乗積表(群表)をつくる。
例:ab=(2341)(3412)=(4123)=c 以下略。  (1) (123) (132) (23) (13) (12) //
(1) (123) (132) (23) (13) (12) //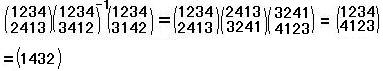 //
//  A4の部分群:K={(1),(12)(34),(13)(24),(14)(23)} について、
e=(1),p=(12)(34),q=(13)(24),r=(14)(23)
とおいたときのKの乗積表を左に示す。
左対角線を軸に対称となり、アーベル群である。
また、Kの中に位数2の部分群:{e,p},{e,q},{e,r}
があることも分る。
A4の部分群:K={(1),(12)(34),(13)(24),(14)(23)} について、
e=(1),p=(12)(34),q=(13)(24),r=(14)(23)
とおいたときのKの乗積表を左に示す。
左対角線を軸に対称となり、アーベル群である。
また、Kの中に位数2の部分群:{e,p},{e,q},{e,r}
があることも分る。
 G'
//
G'
//  HK/Kを得る。 //
HK/Kを得る。 //  右のとおりであり、S2の位数は2。部分群は{e}。
したがって、S2>{e} であり、S2はアーベル群だから可解群である。 //
S3については e=(1), a=(132), b=(123), p=(23), q=(13), r=(12) とおくと、
右のとおりであり、S2の位数は2。部分群は{e}。
したがって、S2>{e} であり、S2はアーベル群だから可解群である。 //
S3については e=(1), a=(132), b=(123), p=(23), q=(13), r=(12) とおくと、
 その乗積表は右のとおりである。
S3の部分群は問
その乗積表は右のとおりである。
S3の部分群は問 {e} であり、
剰余群列S3/A3 , A3/{e} の各位数は 2,3(いずれも素数)。
よって、S3は可解群である。 //
{e} であり、
剰余群列S3/A3 , A3/{e} の各位数は 2,3(いずれも素数)。
よって、S3は可解群である。 // 
 対応する2つの元の交換子 x-1y-1xy を
求めて一覧表をつくると、右のようになる。
それ故、S3の交換子群は { e , a , b } すなわちA3に等しい。
表から、交代群A3={ e , a , b }の交換子群は{e}であることが分る。//
一般にアーベル群の交換子群は{e}である。← x-1y-1xy=(yx)-1xy=(yx)-1yx=e
しかし交換子群は{e}であってもその群がアーベル群であるとは
いえないことも上の表から分る。← {p,q,r}
対応する2つの元の交換子 x-1y-1xy を
求めて一覧表をつくると、右のようになる。
それ故、S3の交換子群は { e , a , b } すなわちA3に等しい。
表から、交代群A3={ e , a , b }の交換子群は{e}であることが分る。//
一般にアーベル群の交換子群は{e}である。← x-1y-1xy=(yx)-1xy=(yx)-1yx=e
しかし交換子群は{e}であってもその群がアーベル群であるとは
いえないことも上の表から分る。← {p,q,r}  cijαiβj ( cij∈k , 0≤i≤2 , 0≤j≤2)
(5)
cijαiβj ( cij∈k , 0≤i≤2 , 0≤j≤2)
(5)  i = (
i = ( とおくと、x-2=
とおくと、x-2=