K = k(θ)をn次の正規拡大体とし、σ,τ,・・・・・・をKの
k-同型対応全体とすればこれらのk-同型対応に次のように乗法を
定義して、1つの群であるようにすることができる.
たとえば、写像σによってα∈Kがσ(α)に写るとき、積τσを
α⇒τ(σ(α))
のような対応であるものと定める. すなわち
τσ(α)=τ(σ(α))
である.このようにして得られた n個の k-同型対応から成る群を
K/kのガロア群といいGal(K/k)と表す.
Kが正則であることから、K のσによる像のσKが集合としてはKに
一致し、したがってσ(α)をKの元と考えることにより、τσ(α)
が意味をもつこととなる.
この関係を図示すればつぎのようになる.
K → σK
=K → τK
α → σ(α) → τσ(α)
ガロア拡大体のk-自己同型対応のことをガロア置換という.
定理1
K/k がガロア拡大体で、L が K、kの中間体であるとき
(すなわち k⊂L⊂Kであるとき)
Lから共役体L'への同値写像は Kの自己同型置換(ガロア
置換)に延長することができる.
|
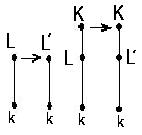 |
註:定理の意味は次のとおりである. すなわち、
Kの部分体Lの同値写像L'が与えられたとき、
Lよりも広い体K からそれ自身への対応(ガ
ロア置換)が存在して、この対応はL'につい
ては始めの対応と同じ対応を与える.
とくにL'はKの部分体である.
|
( 自己流の解釈:Kの部分体Lの同値写像L'が与えられたとき、
そのL'もまたKの部分体である. )
証明
第1段 :
G = Gal(K/k) の置換の中で Lの元をすべて動かさないものの全体
をH とする. このとき K/L がガロア拡大体でそのガロア群が Hに
一致することが証明される.
まず KのL-同型対応は同時に Kの k-同型対応であるからK/kが正則
であるという仮定によりL-同型対応の結果である共役体は集合として
Kと一致する. したがってKのLに関する共役体はKと一致する.
すなわち K/L は正則である.
 K/L のガロア置換は L-自己同型置換であるから
上にも述べたように k-自己同型置換でもある.
したがって Gal(K/L)⊂Gal(K/k) = G である.
すなわち Gal(K/L) の元を求めるには、Gの元の中で
L を不変にするものを求めればよいから Gal(K/L)=H が成り立つ.
K/L のガロア置換は L-自己同型置換であるから
上にも述べたように k-自己同型置換でもある.
したがって Gal(K/L)⊂Gal(K/k) = G である.
すなわち Gal(K/L) の元を求めるには、Gの元の中で
L を不変にするものを求めればよいから Gal(K/L)=H が成り立つ.
|
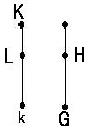
註:ガロア群については G⊃H なることを上の図のように G を
下に H を上に表わした方が便利なことが多い.
第2段 :
[K:L]=m , [L:k}=n とすれば [K:k]=mn である.
今 σをG の任意の元とすれば対応 L→σL は k-同型対応であ
るから σLは Lの共役体である.
この対応L→σLが恒等置換(Lのすべての元を動かさない置換)
となるのは σ∈H の場合である.
G の位数は [H:K]=mn であり、また Hは K/Lのガロア群であるから
その位数は m である.
したがってH の G における指数は mn/m=n である.
このことから G を H の副群に分解したとき副群の個数がn個であ
ることが分る.
G = σ1H+σ2H+・・・・・・+σnH ( σ1=1 )
この際1つの定まった副群 σiHの元σiσ , σiτ (σ,τ∈H)に
よる Lのk-同型対応は、σ,τがLの恒等置換を引き起こすことに注
意すれば、同じ k-同型対応であることが分る.
すなわちσiHの中の置換によって Lのk-同型対応は唯1つしか得ら
れないから、Gの置換によって得られる Lのk-同型置換は高々n個し
かない.
一方もし σiH,σjHの中の置換(たとえばσi,σj) によって Lの同
じ置換が引き起こされるならば、β∈L のとき
σi(β)=σj(β) σj-1σi(β)=β
したがって σj-1σiは L の元を動かさないから
σj-1σi∈H , σi∈σjH
となり σi が副群 σjH に属し σiH = σjH なることが分る.
すなわち
σiH,σjHが Lの同じk-同型置換を引き起こすのはそれらが一致す
る場合に限る.
L/k の k-同型置換は丁度n個存在するからそのいずれもGのどれか
の副群 σiH ( i=1,2,・・・,n )によって引き起こされる同型置換
である. //
|
k[x]における既約多項式 φ(x)の根をα1,α2,・・・,αnとするとき
k( α1,α2,・・・,αn )がkに関して正則であることは前章の定理8
で証明した通りである.
そのガロア群のことを 方程式 φ(x)=0 のガロア群という.
また、k( α1,α2,・・・,αn )=K のことを方程式φ(x)=0に属する
ガロア体という.
K のガロア置換σを与えれば α1,α2,・・・,αn はそれぞれ共役数
α1',α2',・・・,αn' に写り、これは全体としては始めの
α1,α2,・・・,αn と変らない.
したがってガロア置換に対して φ(x)の根の全体の1つの置換が対
応する.
また異なるστがφ(x)の根の同じ置換を引き起こすことは起らない。
何となれば
根 α1,α2,・・・,αnの像が定まればk( α1,α2,・・・,αn )の像が一
意に定まり、ガロア置換が唯1つ決定するからである.
注意しなければならないことは根 α1,α2,・・・,αnの n!個の置換の
全部がガロア置換となるわけではないことである. ココマデcheckスミ6/9
例1.
有理数体 R 上の既約多項式φ(x)=x2 - 2 に属するガロア体
は6次の体になることを前に示した.
この場合は
3つの根  ,ω ,ω ,ω2 ,ω2 のすべての置換がガロア置換となる.
したがってガロア群は3次の対称群である. のすべての置換がガロア置換となる.
したがってガロア群は3次の対称群である.
|
例2.
有理数体 R上の既約多項式 x4+1=0 のガロア群の群表を求めよ.
x4+1 の根はたとえば次のようにして求められる.
(x4-1)(x4 +1)=x8-1
であるから x4+1=0 の根は x8-1=0の根、すなわち1の8乗根の
中でx4-1=0の根とならないものである.
1の冪根の一般論から1の8乗根は右の複素平面上の図のAjに
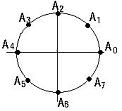 対応する複素数:
対応する複素数: 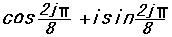 (j=0,1,2,・・・・・・,7)
で与えられる.
ド・モアブルの定理からこれらは
ζj=
(j=0,1,2,・・・・・・,7)
で与えられる.
ド・モアブルの定理からこれらは
ζj= 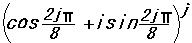 (*1)
と表わすことができる。A1 に相当する1の8乗根は
ζ1= (*1)
と表わすことができる。A1 に相当する1の8乗根は
ζ1=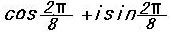 であり、ζj( j=0,1,2,・・・・・・,7 )の中でx4-1=0 の根となるの
はjが偶数の0,2,4,6の場合であることが容易に分るからx4+1=0
の根は ζ,ζ3,ζ5,ζ7 (ζ=ζ1)の4つである.
したがってx4+1=0の根によって生成された体(ζ)の共役体は
R(ζ),R(ζ3),R(ζ5),R(ζ7) (*2)
の4つであるが.ζ3,ζ5,ζ7はR(ζ)の要素であるから
R(ζj) ⊂R(ζ) (j = 3,5,7)
したがって、
(*2)の体のRに対する次数がいずれも4であることから、
R(ζj) = R(ζ) (j=3,5,7)
となり、R(ζ) はそれ自身正則な体であることが示された.
一般に k(α)/k が正則な体で、α=α1,α2,・・・,αnを
α の共役数とすれば、k(αi)=k(α>),αi=k(α>)であるから
αiはαの多項式 fi(α)∈k|α|に等しい。
k(α)/k のガロア群の要素は k(α) からその共役体 k(αi)
へのk-同型対応 σi( i=1,2,・・・,n ) であり、この対応は
α の像αi=fi(α>)が定まれば k(α)の要素 f(α)の像は
f(αi)=f(fi(α>))となって完全に定まる.
したがって正則なk(α)/kのガロア置換は体の置換でなくαの
変換σi:α⇒fi(α>)=αi ( i=1,2,・・・,n )
でああると考えて差し支えない.
f(x)∈k[x] なるとき、
置換σiにより f(α)⇒f(αi) (=f(σi(αi))であることは、
f(α)の像σif(α)が=f(σi(α))であることを示す.
すなわち f(σi(α)=f(σif(α))
とくに、f(x)=fj(x)として σifj(α)=fj(σi(α)
左辺はσi(σj(α))に等しく、右辺は fj(fi(α))に等し
いから (σiσj)(α)=σi(σj(α))=fj(fi(α))
この右辺を計算して fk(α)すなわちσk(α)に等しいことが
分れば σiσj=σk となる.
我々の方程式 x4 + 1 = 0 の場合にはガロア群の要素は
σ1 : ζ⇒ζ=f1(ζ)
σ2 : ζ⇒ζ3=f2(ζ)
σ3 : ζ⇒ζ5=f3(ζ)
σ4 : ζ⇒ζ7=f4(ζ)
となり、これから容易に積 σiσj を求めることができる.
たとえば σ2σ3 については
(σ2σ3)(ζ)=f3(f2(ζ))=f3(ζ3)=(ζ3)5=ζ15
この右辺で ζ8=1 に注意して
であり、ζj( j=0,1,2,・・・・・・,7 )の中でx4-1=0 の根となるの
はjが偶数の0,2,4,6の場合であることが容易に分るからx4+1=0
の根は ζ,ζ3,ζ5,ζ7 (ζ=ζ1)の4つである.
したがってx4+1=0の根によって生成された体(ζ)の共役体は
R(ζ),R(ζ3),R(ζ5),R(ζ7) (*2)
の4つであるが.ζ3,ζ5,ζ7はR(ζ)の要素であるから
R(ζj) ⊂R(ζ) (j = 3,5,7)
したがって、
(*2)の体のRに対する次数がいずれも4であることから、
R(ζj) = R(ζ) (j=3,5,7)
となり、R(ζ) はそれ自身正則な体であることが示された.
一般に k(α)/k が正則な体で、α=α1,α2,・・・,αnを
α の共役数とすれば、k(αi)=k(α>),αi=k(α>)であるから
αiはαの多項式 fi(α)∈k|α|に等しい。
k(α)/k のガロア群の要素は k(α) からその共役体 k(αi)
へのk-同型対応 σi( i=1,2,・・・,n ) であり、この対応は
α の像αi=fi(α>)が定まれば k(α)の要素 f(α)の像は
f(αi)=f(fi(α>))となって完全に定まる.
したがって正則なk(α)/kのガロア置換は体の置換でなくαの
変換σi:α⇒fi(α>)=αi ( i=1,2,・・・,n )
でああると考えて差し支えない.
f(x)∈k[x] なるとき、
置換σiにより f(α)⇒f(αi) (=f(σi(αi))であることは、
f(α)の像σif(α)が=f(σi(α))であることを示す.
すなわち f(σi(α)=f(σif(α))
とくに、f(x)=fj(x)として σifj(α)=fj(σi(α)
左辺はσi(σj(α))に等しく、右辺は fj(fi(α))に等し
いから (σiσj)(α)=σi(σj(α))=fj(fi(α))
この右辺を計算して fk(α)すなわちσk(α)に等しいことが
分れば σiσj=σk となる.
我々の方程式 x4 + 1 = 0 の場合にはガロア群の要素は
σ1 : ζ⇒ζ=f1(ζ)
σ2 : ζ⇒ζ3=f2(ζ)
σ3 : ζ⇒ζ5=f3(ζ)
σ4 : ζ⇒ζ7=f4(ζ)
となり、これから容易に積 σiσj を求めることができる.
たとえば σ2σ3 については
(σ2σ3)(ζ)=f3(f2(ζ))=f3(ζ3)=(ζ3)5=ζ15
この右辺で ζ8=1 に注意して  ζ15=ζ7=f4(ζ)=σ4(ζ)
したがって σ2σ3=σ4 が得られる。
同様の計算によって右の群表が得られる.
ζ15=ζ7=f4(ζ)=σ4(ζ)
したがって σ2σ3=σ4 が得られる。
同様の計算によって右の群表が得られる.
|
次の用語の意味を上の文章の中から読み取って考えよう.
ガロア拡大体:k-同型対応:K/kのガロア群G(K/k):正則:ガロア置換:
同値写像:
|

 K/L のガロア置換は L-自己同型置換であるから
上にも述べたように k-自己同型置換でもある.
したがって Gal(K/L)⊂Gal(K/k) = G である.
すなわち Gal(K/L) の元を求めるには、Gの元の中で
L を不変にするものを求めればよいから Gal(K/L)=H が成り立つ.
K/L のガロア置換は L-自己同型置換であるから
上にも述べたように k-自己同型置換でもある.
したがって Gal(K/L)⊂Gal(K/k) = G である.
すなわち Gal(K/L) の元を求めるには、Gの元の中で
L を不変にするものを求めればよいから Gal(K/L)=H が成り立つ.
 ,ω
,ω 対応する複素数:
対応する複素数: 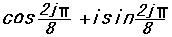 (j=0,1,2,・・・・・・,7)
で与えられる.
ド・モアブルの定理からこれらは
ζj=
(j=0,1,2,・・・・・・,7)
で与えられる.
ド・モアブルの定理からこれらは
ζj= 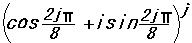 (*1)
と表わすことができる。A1 に相当する1の8乗根は
ζ1=
(*1)
と表わすことができる。A1 に相当する1の8乗根は
ζ1=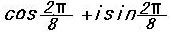 であり、ζj( j=0,1,2,・・・・・・,7 )の中でx4-1=0 の根となるの
はjが偶数の0,2,4,6の場合であることが容易に分るからx4+1=0
の根は ζ,ζ3,ζ5,ζ7 (ζ=ζ1)の4つである.
したがってx4+1=0の根によって生成された体(ζ)の共役体は
R(ζ),R(ζ3),R(ζ5),R(ζ7) (*2)
の4つであるが.ζ3,ζ5,ζ7はR(ζ)の要素であるから
R(ζj) ⊂R(ζ) (j = 3,5,7)
したがって、
(*2)の体のRに対する次数がいずれも4であることから、
R(ζj) = R(ζ) (j=3,5,7)
となり、R(ζ) はそれ自身正則な体であることが示された.
一般に k(α)/k が正則な体で、α=α1,α2,・・・,αnを
α の共役数とすれば、k(αi)=k(α>),αi=k(α>)であるから
αiはαの多項式 fi(α)∈k|α|に等しい。
k(α)/k のガロア群の要素は k(α) からその共役体 k(αi)
へのk-同型対応 σi( i=1,2,・・・,n ) であり、この対応は
α の像αi=fi(α>)が定まれば k(α)の要素 f(α)の像は
f(αi)=f(fi(α>))となって完全に定まる.
したがって正則なk(α)/kのガロア置換は体の置換でなくαの
変換σi:α⇒fi(α>)=αi ( i=1,2,・・・,n )
でああると考えて差し支えない.
f(x)∈k[x] なるとき、
置換σiにより f(α)⇒f(αi) (=f(σi(αi))であることは、
f(α)の像σif(α)が=f(σi(α))であることを示す.
すなわち f(σi(α)=f(σif(α))
とくに、f(x)=fj(x)として σifj(α)=fj(σi(α)
左辺はσi(σj(α))に等しく、右辺は fj(fi(α))に等し
いから (σiσj)(α)=σi(σj(α))=fj(fi(α))
この右辺を計算して fk(α)すなわちσk(α)に等しいことが
分れば σiσj=σk となる.
我々の方程式 x4 + 1 = 0 の場合にはガロア群の要素は
σ1 : ζ⇒ζ=f1(ζ)
σ2 : ζ⇒ζ3=f2(ζ)
σ3 : ζ⇒ζ5=f3(ζ)
σ4 : ζ⇒ζ7=f4(ζ)
となり、これから容易に積 σiσj を求めることができる.
たとえば σ2σ3 については
(σ2σ3)(ζ)=f3(f2(ζ))=f3(ζ3)=(ζ3)5=ζ15
この右辺で ζ8=1 に注意して
であり、ζj( j=0,1,2,・・・・・・,7 )の中でx4-1=0 の根となるの
はjが偶数の0,2,4,6の場合であることが容易に分るからx4+1=0
の根は ζ,ζ3,ζ5,ζ7 (ζ=ζ1)の4つである.
したがってx4+1=0の根によって生成された体(ζ)の共役体は
R(ζ),R(ζ3),R(ζ5),R(ζ7) (*2)
の4つであるが.ζ3,ζ5,ζ7はR(ζ)の要素であるから
R(ζj) ⊂R(ζ) (j = 3,5,7)
したがって、
(*2)の体のRに対する次数がいずれも4であることから、
R(ζj) = R(ζ) (j=3,5,7)
となり、R(ζ) はそれ自身正則な体であることが示された.
一般に k(α)/k が正則な体で、α=α1,α2,・・・,αnを
α の共役数とすれば、k(αi)=k(α>),αi=k(α>)であるから
αiはαの多項式 fi(α)∈k|α|に等しい。
k(α)/k のガロア群の要素は k(α) からその共役体 k(αi)
へのk-同型対応 σi( i=1,2,・・・,n ) であり、この対応は
α の像αi=fi(α>)が定まれば k(α)の要素 f(α)の像は
f(αi)=f(fi(α>))となって完全に定まる.
したがって正則なk(α)/kのガロア置換は体の置換でなくαの
変換σi:α⇒fi(α>)=αi ( i=1,2,・・・,n )
でああると考えて差し支えない.
f(x)∈k[x] なるとき、
置換σiにより f(α)⇒f(αi) (=f(σi(αi))であることは、
f(α)の像σif(α)が=f(σi(α))であることを示す.
すなわち f(σi(α)=f(σif(α))
とくに、f(x)=fj(x)として σifj(α)=fj(σi(α)
左辺はσi(σj(α))に等しく、右辺は fj(fi(α))に等し
いから (σiσj)(α)=σi(σj(α))=fj(fi(α))
この右辺を計算して fk(α)すなわちσk(α)に等しいことが
分れば σiσj=σk となる.
我々の方程式 x4 + 1 = 0 の場合にはガロア群の要素は
σ1 : ζ⇒ζ=f1(ζ)
σ2 : ζ⇒ζ3=f2(ζ)
σ3 : ζ⇒ζ5=f3(ζ)
σ4 : ζ⇒ζ7=f4(ζ)
となり、これから容易に積 σiσj を求めることができる.
たとえば σ2σ3 については
(σ2σ3)(ζ)=f3(f2(ζ))=f3(ζ3)=(ζ3)5=ζ15
この右辺で ζ8=1 に注意して  ζ15=ζ7=f4(ζ)=σ4(ζ)
したがって σ2σ3=σ4 が得られる。
同様の計算によって右の群表が得られる.
ζ15=ζ7=f4(ζ)=σ4(ζ)
したがって σ2σ3=σ4 が得られる。
同様の計算によって右の群表が得られる.
 ,土
,土