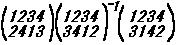群Gの元の個数gをGの位数という。g<∞のときGを有限群という。
今、Gの元aについて冪amを通常のように
a1=a , a2=a･a , a3=a･a･a , ･･････
a-2=(a-1)2 , a-3=( a-1 )3 , ･･････
のように定義する。またa0=eとおけば正または負の整数m,nに対して
aman=am+n
が成立する。
元aの冪の全体はGに含まれる１つの群を作る。
これをaによって生成された群と呼び {a} とあらわす。
もしG={a}ならばGはaを生成元にもつ巡回群という。
一般に群Gの一部分Hがそれ自身群を作るときHは群Gの部分群
という。とくに部分群{a}の位数のことをaの位数という。
群Gの位数と部分群Hの位数についてはつぎの関係がある。
定理２．
Gの部分群Hの位数は Gの位数の約数である。
|
証明： G,Hの位数をそれぞれ g,h とする。今Hの元を
(1) s1,s2,･･････,sh
とするとき、要素の集合
(2) as1,as2,･･････,ash
のことをaの属するHの左副群（または左剰余類、左傍系）
といってaHと表す。
このとき(2)の元がすべて異なることは
asi=asj ならば a-1 を左から乗じてsi=sj
となることから分る。
したがってすべての左副群は同数の元を含む。
もし b が aH の元ならば aH=bH である。
証明：b が aH の元すなわち b=as ならば
bHの任意の元は bsi=assi
ここに s,si はHの元でHは群であるから
ssi はHに属する。
したがってbHの元 bsi はすべてaHに属する。
bHとaHは同数の元を含むから bH=aH である。 //
次に aH , bH が１つの元 c を共有するならば、
上に述べたことから aH = cH , bH = cH であるから
aH = bH である。
したがって
２つの副群は共通な元を持たないか、または完全に一致する
ことがわかった。
以上から G は h個ずつの元を含む副群に分解(類別）されること
が分ったから、副群の個数をjとすれば
g=jh
すなわちhはgの約数であることが証明された。 //
上のj のことをHのGにおける指数といい (G:H) で表す。
元aの位数nは部分群{a} の位数であるから、
上の定理の特別の場合としてnもGの位数の約数である。
{a} の意味から n は a1, a2, a3, ･･････の中で an が
初めて =e となるような自然数である。
例．
H1,H2がGの部分群ならばH1∩H2もGの部分群である。
a , b ∈H1∩H2=H とすれば
a,b∈H1ゆえに 積ab∈H1
同じようにab∈H2だからab∈H1∩H2=H
またa∈Hならばa∈ H1,したがってa-1∈H1
同じ理由でa-1∈H2であるからa-1∈H1∩H2=H
すなわちHの元を２つ乗じてもHの元であり、Hの元に対
してその逆元がHの中にあるのであるが、Hが群であるための
他の条件も明らかであるからHは１つの部分群を作る。//
|
次の用語の定義または意味を上の文章から読み取って答えてみよ。
G の位数： 生成された群H： Hの位数はGの約数： 同型対応：
左副群：副群の個数j, g = jh ：指数 ：左剰余類： １対１対応：
|
および
の回転a,b
(3) 中線に関する折り返しp,q,r。
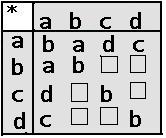
これらの６つの運動について、
先ずaなる運動をして後にbなる運動をすることを積ab
と定義すれば、積abは１つの群を形成する。その結果を下図
のように表に表したものを 群表 という。
G'と表す)
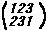と表す。
また置換される数字だけに着目して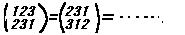
と約束する。
２つの置換の積の計算は
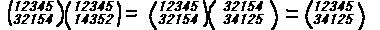の例にならって実行すればよい。
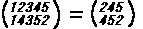のように省略することがある。
１つの置換によってr個の文字が
l1→l2→l3→ ･･････ → lr→l1
のように循環するとき、これをr次の巡回置換といって、簡単に
(l1l2･･････lr ) と表す。
すなわち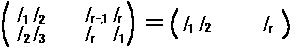 
である。
とくに２次の巡回置換のことを互換という。
任意の巡回置換が互換の積となることは
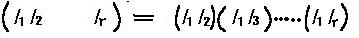なることから分る。( よく理解しておこう。）
次に任意の巡回置換Pにおいて１つの文字l1から始まり
l1→l2,l2→l3 , ･･････
なる置き換えが含まれているとすればlr-1→l1の形の置換も含まれる。
何となれば もし→l1の形の置換が含まれなければ
l2,l3･･････ はすべて異なる文字であるから、
異なる文字が無限に含まれることになる
からである。
l1 , l2 , ･･････ 以外の文字から始まり、同じ操作により
m1→m2 , ･･････ →ms→ m1
なる巡回置換が得られ、P が巡回置換の積として表されることが
分った。前に述べたことからこれらの巡回置換は互換の積である
から、任意の置換は互換の積として表されることが結論できた。
たとえば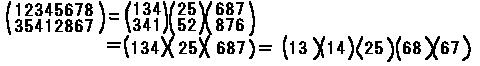 
互換の積としての表し方は１通りとは限らない。たとえば上の置換は
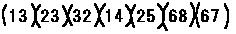とも書き表すこともできる。
しかし、互換の個数に全然法則がないわけではなく、つぎの定理が成立する。
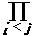(xi- xj) = (x1- x2)(x1- x3)(x1- x4)･･････(x1- xn)
･(x2- x3)(x2- x4)･･････(x2- xn)
･(x3- x4)･･････(x3- xn)
(*1) ･･････
･(xi- xi+1)･･(xi- xn)
･･････
･(xn-1- xn)
x の添数に互換(ij ),(i < j)を施せば F は -F となる。
何となれば
Fの因数の中でx1とx2とを互いに交換すれば、第一の因子(x1 - x2)
は符号が変り、その他の第1行の各因子と第2行の各因子とは互いにそ
の位置を交換し、第3行以下の因子は1つも変らないからF は-F となる。
x1、 x2でなくとも、任意の2つのx、例えばxiとxjとを互いに交換し
てもFは-F になることは見易い。
実際、F において変数x1,･･･,xnの順序を変えてxi,xjを第1、第2の位
置においたときに生ずる式をF'とすれば、F'=±F
しかるにF'において第1、第2の変数であるxiとxjとを交換すれば、
上で述べたように、
F' は -F' になるから、F もやはり -F にならねばならない。
（ 以上の論証は高木貞治著 代数学講義 第5章 27節から引用 ）
Fの因数で変数の添数に置換Pを施せば、上に述べたことから互
換の偶数個の積となるか奇数個の積になるかにしたがってFがF
自身、または-Fに移ることから、Pを２通りの互換の積に分解し
たとき、一方が偶数個で他方が奇数個となることは起こりえない。
//
上の定理により置換Pを互換の偶数個の積となるか奇数個の積となるか
にしたがって偶置換または奇置換と名付けることができる。
n 次の対称群の偶置換の全体は１つの群を作る。これをn次の交代群と
称してここではAnと表わす。
